Formulas
Although most problems cannot be solved through the direct application of a formula, a formula is often helpful in getting to a solution. So, it’s valuable to know the formulas that are likely to be most useful. Here are some important formulas.
Categories of Formulas
Areas – Triangle, Circle, Square, Rectangle, Trapezoid, Sphere, Cylinder
Probability, Combinations, Permutations
Pythagorean Theorem, Sides of 30-60-90, and 45-45-90 Triangles
Volumes – Cube, Cylinder, Sphere, Cone, Pyramid
Individual Formulas
Area of a Circle
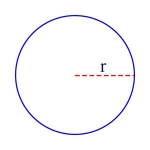\(\begin{align}A = \pi r^2\end{align}\)
In this formula, A is the area of the circle, and r is its radius.
Surface Area of a Cylinder
\(\begin{align}A = 2 \pi r^2 + 2 \pi r h\end{align}\)
or equivalently
\(\begin{align}A = 2 \pi r (r + h)\end{align}\)
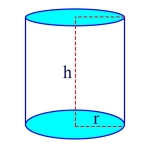In these formulas, A is the surface area of the cylinder, r is the radius of the circles at the top and bottom of the cylinder, and h is the cylinder’s height. For example, if the radius of the cylinder is 2, and the height is 6, then the surface area of the cylinder is
\(\begin{align}2 \pi \times 2 \times (2 + 6) = 32 \pi\end{align}\)
Area of a Rectangle
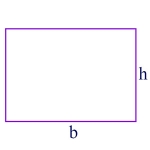
\(\begin{align}A = b \times h\end{align}\)
In this formula, A is the area of the rectangle, b is the length of the base of the rectangle, and h is its height. For example, if b is 6, and h is 4, then
\(\begin{align}A = 6 \times 4 = 24\end{align}\)
Surface Area of a Sphere
\(\begin{align}A = 4 \pi r^2\end{align}\)
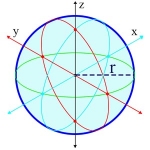
In this formula, A is the surface area of the sphere, and r is its radius. For example, if the radius of a sphere is 2, then its surface area is
\(\begin{align}4 \pi \times 2^2 = 16 \pi\end{align}\)
Area of a Square
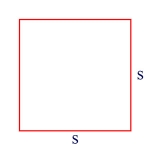
\(\begin{align}A = s^2\end{align}\)
In this formula, A is the area of the square, and s is the length of each side of the square. For example, if the square is 5 on each side, then its area is
\(\begin{align}A = 5^2 = 25\end{align}\)
Area of a Trapezoid
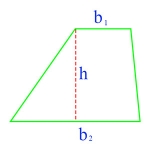
\(\begin{align}A = h \frac{(b_1 + b_2)}{2}\end{align}\)
In this formula, A is the area of the trapezoid, h is the trapezoid’s height, and the b’s are the lengths of its two parallel sides.
Area of a Triangle
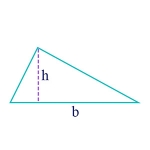
\(\begin{align}A = \frac{1}{2}bh\end{align}\)
In this formula, A is the area of the triangle, h is the height of the triangle, and b is its base. So, for example, if b is 6, and h is 4, then the area is
\(\begin{align}A = \frac{1}{2}(6 \times 4) = 12\end{align}\)
Equation of a Circle
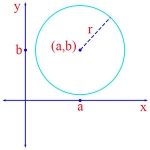
\(\begin{align}(x – a)^2 + (y – b)^2 = r^2\end{align}\)
In this formula, r is the radius of the circle, and the point (a, b) on the coordinate plane is the center of the circle.
Combinations of m things taken n at a time, written as \(\begin{align}m\choose n \end{align}\)
is equal to
\(\begin{align}\frac{m!}{(m-n)!n!}\end{align}\)
Permutations of m things taken n at a time
is equal to
\(\begin{align}\frac{m!}{(m-n)!}\end{align}\)
Probability of an Event
\(\begin{align}\frac{m}{n}\end{align}\)
In this formula, n is the number of possible outcomes, and m is the number of favorable outcomes. For example, the probability that a die will show an even number on its face after being rolled is
\(\begin{align}\frac{3}{6}\end{align}\)
since there are 6 faces on a die and 3 of them show an even number.
Pythagorean Theorem says that in a right triangle, where a and b are the legs and c is the hypotenuse:
\(\begin{align}a^2 + b^2 = c^2\end{align}\)
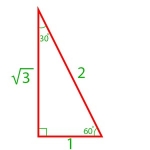
Sides of 30-60-90 Triangle Using the Pythagorean Theorem, and knowing that a 30-60-90 triangle is simply 1/2 of an equilateral triangle, we derive the sides of the triangle as:
\(\begin{align}1, 2, \sqrt{3}\end{align}\)
as shown in the figure.
Sides of 45-45-90 Triangle Using the Pythagorean Theorem, and knowing that a 45-45-90 triangle is isosceles, we derive the sides of the triangle as:
\(\begin{align}1, 1, \sqrt{2}\end{align}\)
as shown in the figure.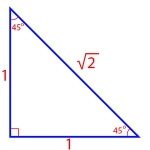
Quadratic Formula All quadratic equations can be solved using the quadratic formula:
\(\begin{align} x = \frac { – b \pm \sqrt {b^2 – 4ac} } {{2a}}\end{align}\)
where the original equation has the form:
\(\begin{align}ax^2 + bx + c = 0\end{align}\)
Slope-Intercept Form The form of the equation of a straight line in which the slope of the line is m, and the point where the line crosses the y-axis, the y-intercept, is b. That is, the general form of this equation is:
\(\begin{align}y = mx + b\end{align}\)
Here’s a specific example:
\(\begin{align}y = 3x + 5\end{align}\)
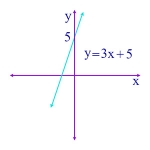
In this example, the slope is 3, and the y-intercept is 5. That is, the line crosses the y-axis at y = 5.
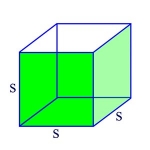
\(\begin{align}V = s^3\end{align}\)
In this formula, V is the volume of the cube, and s is the length of each edge of the cube. For example, if s = 3, then the volume of the cube is
\(\begin{align}3 \times 3 \times 3 = 27\end{align}\)
Volume of a Cone
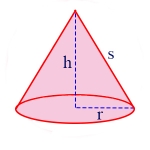\(\begin{align}V = \frac{1}{3} \pi r^2 h\end{align}\)
In this formula, V is the volume of the cone, r is the radius of the circle at the base of the cone, and h is the height of the cone. For example, if r = 2, and h = 6, then the volume of the cone is
\(\begin{align} \frac{1}{3} \pi \times 2^2 \times 6 = 8 \pi\end{align}\)
Volume of a Cylinder
\(\begin{align}V = \pi r^2 h\end{align}\)
In this formula, V is the volume of the cylinder, r is the radius of the circle at the base and the top of the cylinder, and h is the height of the cylinder. For example, if the radius of the cylinder is 2, and the height is 6, then the volume is
\(\begin{align} \pi \times 2^2 \times 6 = 24 \pi\end{align}\)
Volume of a Pyramid
Square base: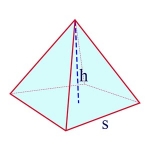
\(\begin{align}V = \frac{1}{3}s^2 h\end{align}\)
In this formula, V is the volume of the pyramid, s is the length of each side of the square at its base, and h is the height of the pyramid.
Triangular base: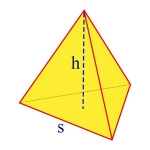
\(\begin{align}V = \frac{1}{12} \sqrt{3}s^2 h\end{align}\)
In this formula, V is the volume of the pyramid, and the base of the pyramid is an equilateral triangle with each side having length s, and where the height of the pyramid is h. For example, the volume of a pyramid with triangular base, with side 2 and height 6 is
\(\begin{align}\frac{1}{12} \sqrt{3} \times 2^2 \times 6 = 2 \times \sqrt{3}\end{align}\)
Volume of a Sphere
\(\begin{align}V = \frac{4}{3}\pi r^3\end{align}\)
In this formula, V is the volume of the sphere, and r is its radius. For example, if a sphere has radius 2, then its volume is
\(\begin{align}\frac{4}{3}\pi \times 2^3 = \frac{32}{3} \times \pi \end{align}\)