Basics of Sets
Click here for definitions of terms
Sets are fundamental to all of mathematics. Intuitively, sets are simply collections of objects, and the individual members of a set are called its elements. If a set has no elements, which is possible, it is called the empty set, and is designated by the symbol ∅.
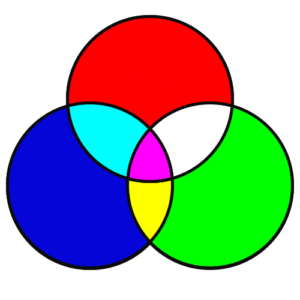
Set are represented graphically using Venn diagrams, in which sets are shown as circles or possibly as rectangles. The Venn diagram in the figure below shows three overlapping sets:
Operations on Sets
We will find these three set operations useful:
- Difference of Sets
- Intersection of Sets
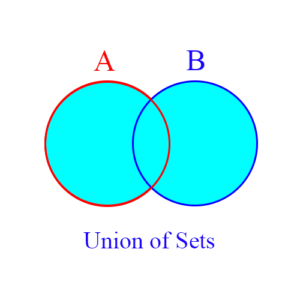
- Union of Sets
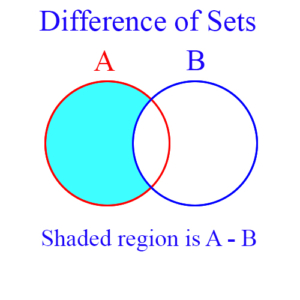
Difference of Sets is an operation on sets that is similar to subtraction of numbers. If A and B are sets, then their difference, A – B, is a new set, defined as all elements of A that are not in B. Obviously, A – B is not necessarily the same as B – A, since A – B is a subset of A, and B – A is a subset of B.
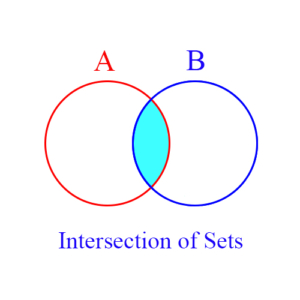
Intersection of Sets: The intersection of two sets is itself a new set, and consists of those elements that are in both sets. For example, suppose A = {1, 2, 3} and B = {2, 3, 4}, then the intersection of A and B is {2, 3} – written A ∩ B = {2, 3}. The blue shaded area in the figure represents the intersection of sets A and B.
Union of Sets is a set operation which from 2 existing sets creates a new set consisting of all elements that are in either or both of the original sets. Example: If A = {1, 2, 3} and B = {2, 3, 4, 5}, then the set union of A and B, written A ∪ B, is {1, 2, 3, 4, 5}.
Two sets are called disjoint or mutually exclusive if they have no elements in common, or in other words their intersection is empty.
Subsets
A subset is a set within a set. That is, all elements of a subset are also in another set. For example, if A = {1, 2, 3} and B = {1, 3}, then B is a subset of A, written B ⊂ A.
The operations on sets we’ve defined above all produce subsets. For example:
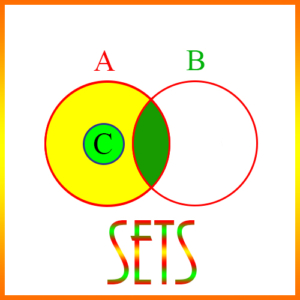
Suppose C = A ∩ B. Then C is a subset of both A and B. Or we could write it as, C ⊂ A, and C ⊂ B.
Suppose C = A ∪ B. Then A and B are both subsets of C. In that case, we write, A ⊂ C, and B ⊂ C.
Suppose C = A – B. Then C ⊂ A. Also, C ∩ B = ∅.
Cardinality of Sets
The number of elements in a set is called the set’s cardinality. If A is a set, then we indicate the cardinality of A by |A|. If A is an infinite set, like the real numbers, then its cardinality is infinite. We will only deal with the cardinality of finite sets. So, for example, if A = {1, 2, 8, 5}, then |A| = 4.
Set cardinality is important in the study of probability. In what follows, assume sets A and B, such that A = {1, 2, 3, 4, 5}, and B = {4, 5, 6, 7}. Then, |A| = 5, and |B| = 4.
Now consider the following cardinalities:
|A ∩ B| = |{4, 5}| = 2
|A – B| = |{1, 2, 3}| = 3
|B – A| = |{6, 7}| = 2
|A ∪ B| = |{1, 2, 3, 4, 5, 6, 7}| = 7
From these examples it’s easy to see how the following general rules can be derived:
- |A – B| = |A| – |A ∩ B|
- |A ∪ B| = |A| + |B| – |A ∩ B|
- |A ∩ B| = |A| + |B| – |A ∪ B|
Using the cardinalities given above for each of these sets, we see that statement 1 is equivalent to:
|A – B| = |A| – |A ∩ B|
3 = 5 – 2
And statement 2 is equivalent to:
|A ∪ B| = |A| + |B| – |A ∩ B|
7 = 5 + 4 – 2
Finally, statement 3 is equivalent to:
|A ∩ B| = |A| + |B| – |A ∪ B|
2 = 5 + 4 – 7
Statements 1, 2, and 3 apply to all sets, not just the examples we’ve given here for A and B.