Combinations/Probability
Every Data Sufficiency (DS) question can have 1 of 5 possible answers, and the possible answers are the same for every DS question. All DS questions are really two questions in one. You’re given a general problem, followed by two supplemental statements. The real problem is to evaluate each of the two statements independently to determine their individual sufficiency to solve the original general problem. As you determine the sufficiency of these statements, you are able to decide which of the following 5 answers to the Data Sufficiency question is the correct answer:
A. Statement 1 is sufficient, but statement 2 is not.
B. Statement 1 is not sufficient, but statement 2 is.
C. Neither statement 1 nor statement 2 is sufficient, but together they are.
D. Both statement 1 and statement 2 are individually sufficient.
E. Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
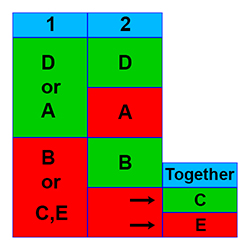
The diagram above gives a pictorial representation of the 5 Data Sufficiency answers. The two statement numbers are shown in blue at the top of the first two columns. Note that green means sufficient, and red means not sufficient. As an example, if both statements 1 and 2 are individually sufficient, then the correct answer is D. For more information on the 5 DS answers, see our videos.
We illustrate these answers for probability problems with the following 2 examples. Each of these examples provides 5 different versions of supplementary statements for the same general problem, and each of these 5 versions yields a different one of the 5 possible answers. The answers to these 5 versions are explained immediately after the problem.
[Notice that the 5 versions of the supplementary statements provide examples of the 5 different answers, A – E. However, they are not given in A – E order.]
Example 1)
At a banquet Ynez is considering two different types of pie for dessert – peach pie and blackberry pie. What is the probability she will have slices of both?
Version I.
(1) The probability she’ll have peach is 50%.
(2) The probability she’ll have neither is 10%, and the probability that she will have peach only or blackberry only is 70%.
Version II.
(1) The probability she’ll have neither is 10%, and the probability that she will have peach only or blackberry only is 70%.
(2) The probability she’ll have neither or only one is 80%.
Version III.
(1) The probability she’ll have neither is 10%, and the probability that she will have peach only or blackberry only is 70%.
(2) The probability she’ll have blackberry is 60%.
Version IV.
(1) The probability she’ll have neither is 10%.
(2) The probability she’ll have peach only or blackberry only is 70%.
Version V.
(1) The probability she’ll have blackberry is 60%.
(2) The probability she’ll have peach is 50%.
Answers: [ Version I: B Version II: D Version III: A Version IV: C Version V: E ]
Explanation:
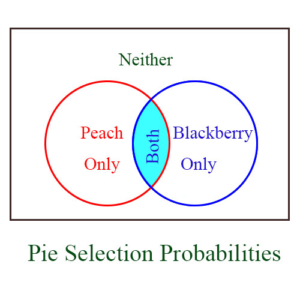
This problem shows a direct connection between set theory and probability calculation – a connection which is very common. The possible probabilities to deal with here are: Neither, Blackberry only, Peach only, or Both, as shown in the Venn diagram below. These are all the possible individual probabilities, and the four are mutually exclusive, so their probabilities are additive – that is, a given probability could be the sum of two, three, or all four of them. The sum of all 4 probabilities is 1. This problem is asking for the probability of Both, which we can determine, for example, by subtracting the other 3 probabilities from 1.
From the supplementary statements for the 5 different versions we can calculate these individual probabilities as follows:
- Neither = 10%
- Peach Only = 30%
- Blackberry Only = 40%
- Both = 20%
Note that the various supplementary statements reflect this information or combinations of probabilities taken from this information. For example, the probability of Ynez selecting Peach is the sum of Peach Only and Both, or 30% + 20% = 50%.
Version I: Answer B – Statement 1 is not sufficient, but statement 2 is.
(1) The probability she’ll have peach is 50%.
Partial information. Note that this is “peach,” not “peach only.” We still need to know (among other things) the probability of neither. Not sufficient.
(2) The probability she’ll have neither is 10%, and the probability that she will have peach only or blackberry only is 70%.
Full information. This accounts for 80% of the probability. The remaining 20% is the probability of her having both. Sufficient.
Version II: Answer D – Both statement 1 and statement 2 are individually sufficient.
(1) The probability she’ll have neither is 10%, and the probability that she will have peach only or blackberry only is 70%.
Full information. This accounts for 80% of the probability. The remaining 20% is the probability of her having both. Sufficient.
(2) The probability she’ll have neither or only one is 80%.
Full information. The remaining 20% is the probability of her having both. Sufficient.
Version III: Answer A – Statement 1 is sufficient, but statement 2 is not.
(1) The probability she’ll have neither is 10%, and the probability that she will have peach only or blackberry only is 70%.
Full information. This accounts for 80% of the probability. The remaining 20% is the probability of her having both. Sufficient.
(2) The probability she’ll have blackberry is 60%.
Partial information. Note that this is “blackberry,” and not “blackberry only.” We still need to know several other probabilities. Not sufficient.
Version IV: Answer C – Neither statement 1 nor statement 2 is sufficient, but together they are.
(1) The probability she’ll have neither is 10%.
Partial information. We still need probabilities for peach and blackberry only. Not sufficient.
(2) The probability she’ll have peach only or blackberry only is 70%.
Partial information. We still need the probability of neither. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because this accounts for 80% of the probability. The remaining 20% is the probability of her having both.
Version V: Answer E – Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
(1) The probability she’ll have blackberry is 60%.
Partial information. Note that this is “blackberry,” not “blackberry only.” We still need to know (among other things) the probability of neither. Not sufficient.
(2) The probability she’ll have peach is 50%.
Partial information. Note that this is “peach,” not “peach only.” We still need to know (among other things) the probability of neither. Not sufficient.
Alone, neither of these statements is sufficient, and together they are not sufficient, because we still need to know the probability of neither, as well as the probability of blackberry only and peach only.
To practice more problems like this, click here.
Example 2)
There are k boys and m girls in a class. The teacher selects two students at random. What is the probability that two girls will be selected?
Version I.
(1) If the first two selected are girls, there will still be more girls left than boys.
(2) There are 18 class members, and 4 more girls than boys.
Version II.
(1) There are fewer than 30 class members, and 7/18 of them are boys.
(2) If the first one selected is a girl, then there will be 10 girls left.
Version III.
(1) There are 18 class members, and 4 more girls than boys.
(2) There are fewer than 30 class members, and 7/18 of them are boys.
Version IV.
(1) There are 18 class members.
(2) There are 4 more girls than boys.
Version V.
(1) If the first one selected is a girl, then there will be 10 girls left.
(2) If the first two selected are girls, there will still be more girls left than boys.
Answers: [ Version I: B Version II: A Version III: D Version IV: C Version V: E ]
Explanation:
If we know the total number of students and either the number of girls or the number of boys, we can compute the probability of each random selection. The probability of choosing a girl on the first selection is m/(k + m), and on the second selection (assuming a girl was chosen on the first selection) is (m-1)/(k + m – 1). The probability of both of these happening is their product.
Version I: Answer B – Statement 1 is not sufficient, but statement 2 is.
(1) If the first two selected are girls, there will still be more girls left than boys.
Partial information. This is a comparative statement and gives us no specific numbers from which we can compute probability. Not sufficient.
(2) There are 18 class members, and 4 more girls than boys.
Full information. From this we deduce that there are 11 girls and 7 boys. Now we can figure the probability that the first two selected are girls. Sufficient.
Version II: Answer A – Statement 1 is sufficient, but statement 2 is not.
(1) There are fewer than 30 class members, and 7/18 of them are boys.
Full information. If 7/18 are boys, then there must be 18 class members, including 7 boys, since the number of each must be an integer, and the next highest integer from which 7/18 can result must be 36. So 7 of the class members are boys, and 11 are girls. From this we can compute the probability. Sufficient.
(2) If the first one selected is a girl, then there will be 10 girls left.
Partial information. We now know there are 11 girls, but we don’t know the total number of students. Not sufficient.
Version III: Answer D – Both statement 1 and statement 2 are individually sufficient.
(1) There are 18 class members, and 4 more girls than boys.
Full information. From this we deduce that there are 11 girls and 7 boys. Now we can figure the probability that the first two selected are girls. Sufficient.
(2) There are fewer than 30 class members, and 7/18 of them are boys.
Full information. If 7/18 are boys, then there must be 18 class members, including 7 boys, since the number of each must be an integer, and the next highest integer from which 7/18 can result must be 36. So 7 of the class members are boys, and 11 are girls. From this we can compute the probability. Sufficient.
Version IV: Answer C – Neither statement 1 nor statement 2 is sufficient, but together they are.
(1) There are 18 class members.
Partial information. We need the girl-boy breakdown in numbers. Not sufficient.
(2) There are 4 more girls than boys.
Partial information. We need to know the total number of students. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because from these we deduce that there are 11 girls and 7 boys. Now we can figure the probability that the first two selected are girls.
Version V: Answer E – Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
(1) If the first one selected is a girl, then there will be 10 girls left.
Partial information. We now know there are 11 girls, but we don’t know the total number of students. Not sufficient.
(2) If the first two selected are girls, there will still be more girls left than boys.
Partial information. This is a comparative statement and gives us no specific numbers from which we can compute probability. Not sufficient.
Alone, neither of these statements is sufficient, and together they are not sufficient, because neither statement tells us the number of boys or the total number of students.
To practice more problems like this, click here.