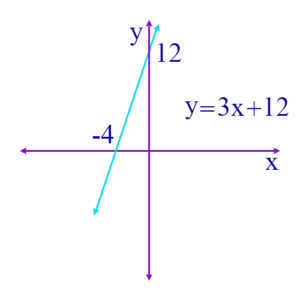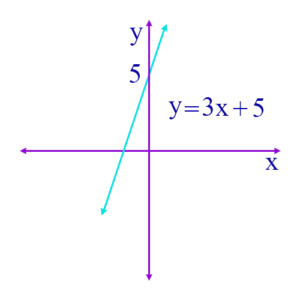Definitions
Often, the answer to a question is obvious if you just know the definition of some term in the question. So, it’s very important to know the definitions of all the terms in the questions! Here are some important definitions, given in alphabetical order.
List of Terms
Absolute Value, Acute Angle, Acute Triangle, Altitude, Arithmetic Mean, Average, Base of a Cylinder, Base of a Triangle, Cardinality of a Set, Center of a Circle, Circle, Circumference of a Circle, Circumscribed Circle, Circumscribed Polygon, Coefficient, Combinations, Complementary Angles, Conditional Probability, Cone, Congruent Triangles, Consecutive Even Integers, Consecutive Integers, Consecutive Odd Integers, Constant, Coordinate Axes, Coordinate Plane, Coordinates, Cube, Cylinder, Data Interpretation Problem, Decimal Number, Decimal Point, Denominator, Diameter of a Circle, Difference of Sets, Discount/Markup Word Problem, Disjoint Sets, Divisible, Divisor, Domain of a Function, Edge of a Solid Figure, Element of a Set, Empty Set, Endpoints of a Line Segment, Equally Likely Probability, Equation, Equilateral Triangle, Equivalent Equations, Equivalent Fractions, Even Integer, Event, Experiment, Exponent, Expression, Face of a Geometric Solid, Factor, Factorial, Factorization of Polynomials, Fraction, Frequency Distribution, Function, Geometry Word Problem, Greatest Common Factor (Divisor), Hexagon, Hypotenuse, Impossible Probability, Improper Fraction, Independent Equations, Independent Events, Inequality, Inscribed Circle, Inscribed Polygon, Integer, Intercept, Interest Word Problem, Intersection of Sets, Inverse, Irrational Number, Isosceles Triangle, Least Common Multiple, Legs of a Right Triangle, Line, Line Segment, Linear Equation, Mean, Measurement Word Problem, Median, Mixture Word Problem, Mode, Monomial, Multiple, Mutually Exclusive Sets, Natural Number, Numerator, Obtuse Angle, Obtuse Triangle, Odd Integer, Origin, Outcome, Parabola, Parallel Lines, Parallelogram, Pentagon, Percent, Perimeter, Permutations, Perpendicular Lines, Point of Tangency, Point on the Coordinate Plane, Polygon, Polynomial, Power, Prime Factorization, Prime Number, Probability, Product, Profit Word Problem, Proportion, Pyramid, Pythagorean Theorem, Quadrants, Quadratic Equation, Quadratic Formula, Quadrilateral, Quotient, Radius of a Circle, Range of a Function, Range of a Set of Values, Rate Word Problem, Ratio, Rational Number, Real Number, Reciprocal, Rectangle, Rectangular Solid, Remainder, Repeating Decimal, Right Angle, Right Triangle, Root of a Number, Roots of an Equation, Scalene Triangle, Scientific Notation, Secant, Sequence, Set, Set Word Problem, Sides of Geometric Figures, Similar Triangles, Simultaneous Linear Equations, Slope, Slope-Intercept Form, Solutions to an Equation, Special Triangles, Sphere, Square, Square Root, Standard Deviation, Statistical Function, Subset, Supplementary Angles, Surface Area, Tangent, Term, Transversal, Trapezoid, Triangle, Union of Sets, Unknown Quantity, Variable, Variance, Venn Diagram, Vertex, Vertical Angles, Volume, Word Problem, Work Word Problem, x-axis, x-coordinate, x-intercept, y-axis, y-coordinate, y-intercept
Individual Terms and Their Definitions
Absolute Value: The distance a number is from 0. If x is a positive real number, then its absolute value, |x|, is x. For example, if x is 3, then |x| = |3| = 3. If x is a negative real number, then |x| = -x. For example, if x is -3, then |x| = |-3| = -(-3) = 3. Notice that both 3 and -3 are the same distance, 3, from 0.
See also Function, Inequality
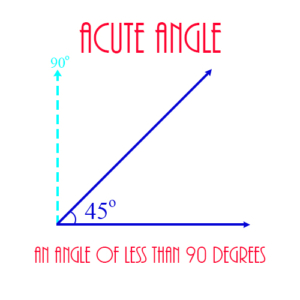
Acute Angle: An angle of less than 90 degrees. The figure shows an example, in this case the angle is 45°.
See also Right, Obtuse, Vertical, Complementary, Supplementary
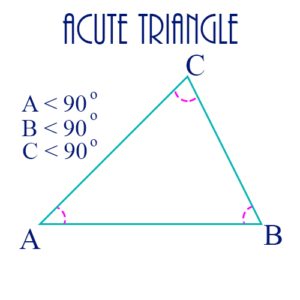
Acute Triangle: A triangle having 3 acute angles.
See also Right, Equilateral, Isosceles, Scalene, Obtuse, Similar, Congruent
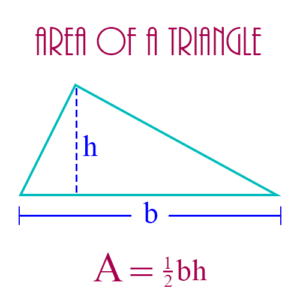
Altitude: In a triangle, an altitude is a line segment that extends from one vertex to the side opposite the vertex, and which is perpendicular to that side. The figure shows the altitude of a triangle, designated as h (for “height”), extending from the top vertex to the side opposite that vertex, designated as b (for “base”). The formula for the area of the triangle makes use of the altitude, as shown.
See also Base of a Triangle, Triangle
Arithmetic Mean: The average of a list of values, in which there could be repetitions. For example, if L = 3, 7, 3, 4, 3 is a list of values, then the arithmetic mean of L is (3 + 7 + 3 + 4 + 3)/5 = 20/5 = 4.
See also Average, Frequency Distribution, Mean, Median, Mode, Standard Deviation, Statistical Function
Average: If L = 3, 7, 3, 4, 3 is a list of values, then the average of L is the sum of its values divided by the number of values in the list.
See also Arithmetic Mean, Frequency Distribution, Mean, Median, Mode, Standard Deviation, Statistical Function
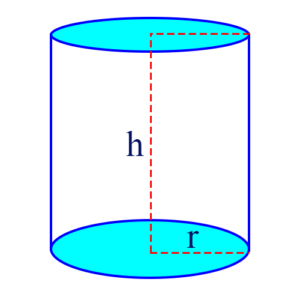
Base of a Cylinder: One of the two circles that form the top or the bottom of a cylinder. The figure shows the two bases shaded blue.
See also Cone, Cube, Cylinder, Pyramid, Sphere
Base of a Triangle: The side of a triangle to which an altitude is perpendicular, used to calculate the area of the triangle. If h is an altitude, and b is its corresponding base, then the area A of the triangle is calculated by A = ½bh. The figure shows the base of a triangle, designated as b, to which the line h (for “height”) extends from the top vertex.
Cardinality of a Set: The number of elements in a set.
See also Difference of Sets, Element of a Set, Empty Set, Intersection of Sets, Set, Set Word Problem, Union of Sets, Venn Diagram
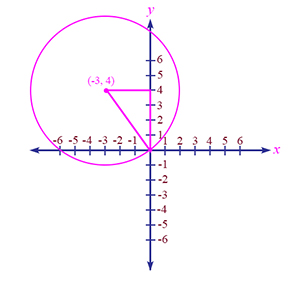
Center of a Circle: The point in the middle of the circle that is equidistant from all the points on the circle. The figure shows a circle of radius 5 on the coordinate plane, with its center at the point (-3, 4).
See also Circle, Circumscribed Circle, Circumscribed Polygon, Inscribed Circle, Inscribed Polygon, Radius, Diameter, Circumference, Tangent, Secant
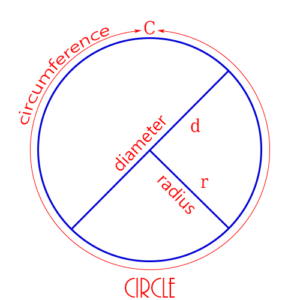
Circle: A set of points equidistant from a given point. The given point is the center of the circle, and the distance from the center to any point on the circle is the radius. The figure shows a circle of radius 5 on the coordinate plane, with its center at the point (-3, 4).
See also Circumscribed Circle, Circumscribed Polygon, Inscribed Circle, Inscribed Polygon, Center, Radius, Diameter, Circumference, Tangent, Secant
Circumference of a Circle: The distance around (or the perimeter of) the circle.
Given by the formula:
\(\begin{align} C = \pi d\end{align}\)
where d is the diameter of the circle, and \(\begin{align}\pi\end{align}\) is a constant value approximately equal to 3.14.
See also Circle, Circumscribed Circle, Circumscribed Polygon, Inscribed Circle, Inscribed Polygon, Center, Radius, Diameter, Tangent, Secant
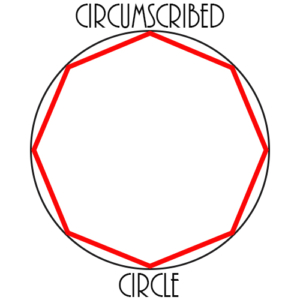
Circumscribed Circle: A circle which is drawn around a polygon in such a way that all the vertices of the polygon are on the circle. In this case the polygon is inscribed in the circle. The figure shows a circle circumscribed around an octagon.
See also Circle, Circumscribed Polygon, Inscribed Circle, Inscribed Polygon, Center, Radius, Diameter, Circumference, Tangent, Secant
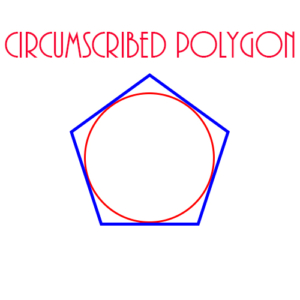
Circumscribed Polygon: A polygon drawn around a circle in such a way that each side of the polygon is tangent to the circle. In this case, the circle is inscribed in the polygon.
See also Circle, Circumscribed Circle, Inscribed Circle, Inscribed Polygon, Center, Radius, Diameter, Circumference, Tangent, Secant
Coefficient: The constant value in a term containing a variable. For example, 2x is a term, and 2 is the coefficient in this term. In the polynomial
\(\begin{align}3x^2 + 5x + 9\end{align}\)
3 is the coefficient of the first term, and 5 is the coefficient of the second term.
See also Constant, Variable, Term, Monomial, Product, Factorization
Combinations: Groupings of a set of objects without regard to order. For example, there are 7 different combinations of the elements in the set {1, 2, 3}: {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, and {1, 2, 3}. Notice that in all of these the order in which they are listed is not important. Thus, for example, the set {1, 2} is exactly the same set as {2, 1}. This is in contrast to permutations, where order is important.
There are 3 combinations of these elements if we take them just 2 at a time: {1, 2}, {1, 3}, {2, 3}. Another way of saying this is that the number of combinations of 3 things, taken 2 at a time, is 3.
The number of combinations of n things taken p at a time is given by the formula
\(\begin{align} \frac {n!}{(n-p)!p!}\end{align}\)
\(\begin{align} n \choose p\end{align}\)
which is said, “n choose p.” If n is 3 and p is 2, then this formula becomes:
\(\begin{align} \frac {3!}{(3-2)!2!} = \frac {3!}{2!} = \frac {3 \times 2 \times 1}{2 \times 1} = 3\end{align}\)
See also Probability, Permutations, Factorial
Complementary Angles: Two angles whose sum is 90 degrees.
See also Acute, Right, Obtuse, Vertical, Supplementary Angles
Conditional Probability: The probability that a given event will occur if it’s known that some other event has occurred. For example, if an ace has been drawn from a pack of 52 cards, conditional probability determines the probability that another ace will be drawn.
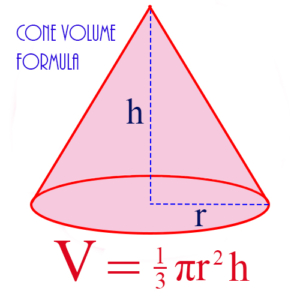
Cone: A 3-dimensional geometric figure whose base is a circle, and which moves up from the base until it converges to a single point. Its volume is calculated from the formula:
\(\begin{align} V = \frac{1}{3} \pi r^2 h\end{align}\)
where r is the radius of the circle at the base, and h is the height from the base to the point at the top.
See also Base of a Cylinder, Cube, Cylinder, Pyramid, Sphere
Congruent Triangles: Two triangles which are exactly equal in their corresponding sides and angles. The figure below shows two congruent triangles, one on the left, the other on the right, created by dividing an equilateral triangle in half. Note the equality of corresponding parts: Each triangle has a side of length 1 and a side of length 2. The vertical line in the middle is a side common to both triangles. Also, the three angles of both triangles are equal to each other: Each triangle has an angle of size 60° and an angle of 30°. Finally, the angle the vertical line makes with the base of the triangle is a right angle for each triangle.
See also Acute, Right, Equilateral, Isosceles, Scalene, Obtuse, Similar
Consecutive Even Integers: A sequence of even integers, each element of which is 2 greater than the previous element. Examples:
8, 10, 12, 14, 16, …
-4, -2, 0, 2, 4, 6, …
See also Consecutive Integers, Consecutive Odd Integers, Divisible, Divisor, Even Integer, Integer, Multiple, Odd Integer, Quotient, Remainder
Consecutive Integers: A sequence of integers, each element of which is 1 greater than the previous element. Examples:
0, 1, 2, 3, 4, …
-3, -2, -1, 0, 1, 2, …
See also Consecutive Even Integers, Consecutive Odd Integers, Divisible, Divisor, Even Integer, Integer, Multiple, Odd Integer, Quotient, Remainder
Consecutive Odd Integers: A sequence of odd integers, each element of which is 2 greater than the previous element. Examples:
7, 9, 11, 13, 15, …
-5, -3, -1, 1, 3, …
See also Consecutive Even Integers, Consecutive Integers, Divisible, Divisor, Even Integer, Integer, Multiple, Odd Integer, Quotient, Remainder
Constant: A fixed value, either a real, imaginary, or complex number. It may be a term in a polynomial. The coefficients in polynomial terms are constants. An unspecified constant is usually indicated by a letter from the beginning of the alphabet, like a, b, or c.
See also Coefficient, Variable, Term, Monomial, Product, Factorization
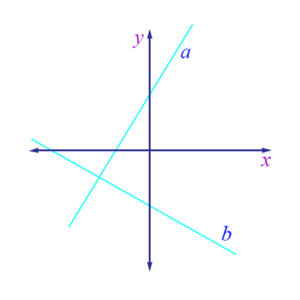
Coordinate Axes: The straight lines, one horizontal (the x-axis), and the other vertical (the y-axis), that define a plane (the Coordinate Plane) for graphing equations. Every real number is on each of these two axes, and the point – called the Origin – at which the axes intersect is 0 on both axes. Moving to the right on the x-axis, the numbers increase, and moving to the left they decrease. Moving up on the y-axis numbers increase, and moving down they decrease. Every point on the coordinate plane has an x-coordinate and a y-coordinate – two real numbers which define exactly where the point is on the plane. The figure shows the x and y axes with two lines, a and b.
See also Coordinates, Quadrants, Origin, Point, Line, Slope, Intercept, x-axis, x-coordinate, x-intercept, y-axis, y-coordinate, y-intercept
Coordinate Plane: See Coordinate Axes
Coordinates: An ordered pair of real numbers (x, y) which identify a point on the coordinate plane. For example, in the figure the coordinates (-3, 4) identify the point which is 3 units to the left of the y-axis and 4 units above the x-axis. This point is the center of a circle of radius 5.
See also Coordinate Axes, Quadrants, Point, Line, Slope, Intercept, x-axis, x-coordinate, x-intercept, y-axis, y-coordinate, y-intercept
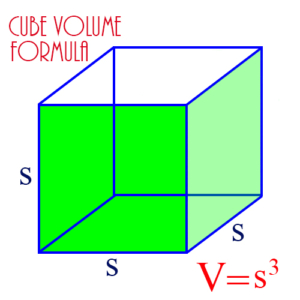
Cube: A 3-dimensional figure of 6 sides, each of which is a square with the same dimensions. Each line where two faces meet is called an edge, and each edge has the same length. The cube’s volume is given by the formula:
\(\begin{align} V = s^3\end{align}\)
where s is the length of each edge of the cube.
See also Base of a Cylinder, Cone, Cylinder, Pyramid, Sphere
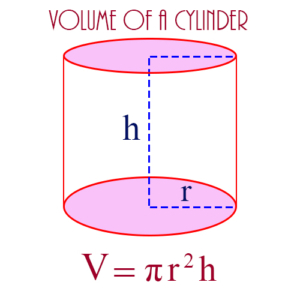
Cylinder: A 3-dimensional figure whose base is a circle, and which continues straight up to height h until it ends in a circle of the same size as the base. Its volume is given by the formula:
\(\begin{align} V = \pi r^2 h\end{align}\)
where r is the radius of the base circle, and h is the height of the cylinder.
See also Base of a Cylinder, Cone, Cube, Pyramid, Sphere
Data Interpretation Problem: A word problem whose basis is a set of data given in a table or on a graph.
See also Discount/Markup Word Problem, Geometry Word Problem, Interest Word Problem, Measurement Word Problem, Mixture Word Problem, Profit Word Problem, Rate Word Problem, Set Word Problem, Word Problem, Work Word Problem
Decimal Number: A number defined using the decimal or base ten system. Its decimal point separates the integer part from the fractional part, with each numeral to the right of the decimal representing some negative power of 10, and each numeral to the left representing some non-negative power of 10. Example:
8,765.4321
In this example, 8 is in the 1000’s (or 103) position, 7 in the 100’s (102) position, etc.
We say that 5 is in the “units” position, and 4 is in the tenths or 10-1 position.
See also Decimal Point, Fraction, Percent, Rational Number, Repeating Decimal, Scientific Notation
Decimal Point: The dot or period in a decimal number which separates the integer part on the left from the fractional part on the right.
See also Decimal Number, Fraction, Percent, Rational Number, Repeating Decimal, Scientific Notation
Denominator: The bottom number in a fraction. Example: The denominator of 2/3 is 3.
Diameter of a Circle: Any line segment from one point on the circle to a point on the opposite side of the circle, passing through the center of the circle. Its length (also called “the diameter”) is always twice the length of a radius.
See also Radius, Circumference, Tangent, Secant, Circle
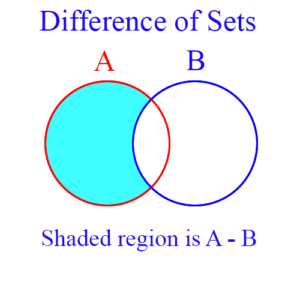
Difference of Sets: An operation on sets that is similar to subtraction of numbers. If A and B are sets, then their difference, A – B, is a new set, defined as all elements of A that are not in B. Obviously, A – B is not necessarily the same as B – A, since A – B is a subset of A, and B – A is a subset of B.
See also Cardinality of a Set, Element of a Set, Empty Set, Intersection of Sets, Set, Set Word Problem, Union of Sets, Venn Diagram
Discount/Markup Word Problem: A word problem that uses the concept of discounting prices of products. Example: If the price of a television is discounted from $200 to $150, then the price has been discounted by 50/200, or 25%.
See also Data Interpretation Problem, Geometry Word Problem, Interest Word Problem, Measurement Word Problem, Mixture Word Problem, Profit Word Problem, Rate Word Problem, Set Word Problem, Word Problem, Work Word Problem
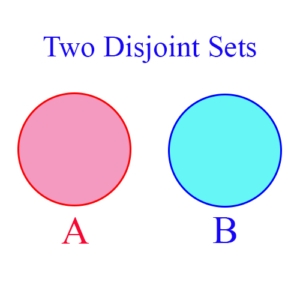
Disjoint Sets: Sets which have no common elements are disjoint. This is usually shown by stating their intersection is empty. So, for example, if A and B are disjoint sets, then A ∩ B = ∅. As a specific example, if A = {1, 2} and B = {3, 4, 5}, then A ∩ B = ∅. The figure is a Venn diagram showing that sets A and B don’t overlap or intersect.
See also Cardinality of a Set, Difference of Sets, Element of a Set, Empty Set, Intersection of Sets, Set, Set Word Problem, Union of Sets, Venn Diagram
Divisible: This states a relationship between two integers. a is divisible by b, if for some integer n, a = bn.
See also Consecutive Even Integers, Consecutive Integers, Consecutive Odd Integers, Divisor, Even Integer, Integer, Multiple, Odd Integer, Quotient, Remainder
Divisor: This states a relationship between two integers. b is a divisor of a, if for some integer n, a = bn.
See also Consecutive Even Integers, Consecutive Integers, Consecutive Odd Integers, Divisible, Even Integer, Integer, Multiple, Odd Integer, Quotient, Remainder
Domain of a Function: The set of values on which the function is defined. For example, a sequence is usually defined on the non-negative integers. Therefore, the domain of a sequence is the non-negative integers.
See also Function, Range of a Function
Edge of a Solid Figure: A solid figure, like a cube, has multiple faces which meet to form the solid. The lines where they meet are edges. Examples: A cube has 6 faces, and each face is a square. The sides of each square are edges of the cube. The figure shows a cube with 3 edges marked as s. As you can see, a cube has 12 edges altogether.
See also Face of a Geometric Solid, Sides of Geometric Figures, Surface Area, Volume
Element of a Set: A single member of a set. Examples: If the set A = {1, 2, 3}, then 1, 2, and 3 are its elements. The negative whole numbers are elements of the set of integers. Other elements of the set of integers are 0 and the positive whole numbers.
See also Cardinality of a Set, Difference of Sets, Empty Set, Intersection of Sets, Set, Set Word Problem, Union of Sets, Venn Diagram
Empty Set: This a set which has no elements. This may seem counter-intuitive, because sets are collections of objects, but the empty set comes in handy. For example, suppose you take the intersection of two disjoint sets. Since they’re disjoint, their intersection will have no elements in it. But the intersection of any two sets is a new set. So the intersection of two disjoint sets must be a set. It is in fact a set – the empty set. The empty set is usually denoted by the symbol ∅. Example: If two sets, A and B, are disjoint, then A ∩ B = ∅.
See also Cardinality of a Set, Difference of Sets, Element of a Set, Intersection of Sets, Set, Set Word Problem, Union of Sets, Venn Diagram
Endpoints of a line segment: The two points – the red dots in the figure below – which mark the beginning and end of a line segment.
See also Line Segment
Equally Likely Probability: If several events in a probability experiment are equally likely or probable to occur, then these events have equally likely probability. Example: The two sides of a normal coin are equally likely to turn up when the coin is tossed, and so heads and tails have the equally likely probability of 1/2.
See also Event, Experiment, Impossible Probability, Independent Events, Outcome, Probability
Equation: An algebraic statement that shows two algebraic expressions separated by an equals sign. This signifies that the value on the left of the equals sign is the same as the value on the right. Example: 3x – 5 = 2x + 9. This equations states that the expression on the left, 3x – 5, is equal to the expression on the right, 2x + 9. When we solve this equation, we determine that these two expressions can only be equal when x = 14.
See also Equivalent Equations, Expression, Independent Equations, Inequality, Linear Equation, Polynomial, Quadratic Equation, Quadratic Formula, Roots of an Equation, Simultaneous Linear Equations, Solutions to an Equation, Unknown Quantity, Variable
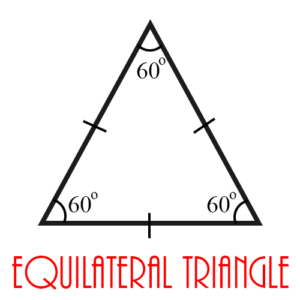
Equilateral Triangle: A triangle whose 3 sides have equal length.
See also Acute, Right, Isosceles, Scalene, Obtuse, Similar, Congruent
Equivalent Equations: Two equations are equivalent if one can be transformed to the other by a simple operation, such as multiplying both sides of the equation by the same value. Example: 2x + 7 = y is equivalent to 4x + 14 = 2y, because if we multiply both sides of the first equation by 2, then we obtain the second equation. If one equation is equivalent to another, then the second equation gives us no new information that we didn’t already have in the first equation. Every solution to one equation is also a solution to the other. If two equations are not equivalent, then they are said to be independent.
See also Equation, Expression, Independent Equations, Inequality, Linear Equation, Polynomial, Quadratic Equation, Quadratic Formula, Roots of an Equation, Simultaneous Linear Equations, Solutions to an Equation, Unknown Quantity, Variable
Equivalent Fractions: Two fractions are equivalent if one can be transformed to the other by simply multiplying both numerator and denominator by the same number. Example: 1/2 is equivalent to 4/8, because if numerator and denominator of 1/2 is multiplied by 4, we get 4/8.
See also Fraction
Even Integer: An integer divisible by 2. Examples: 0, 2, 4, 6, 8.
See also Consecutive Even Integers, Consecutive Integers, Consecutive Odd Integers, Divisible, Divisor, Integer, Multiple, Odd Integer, Quotient, Remainder
Event: A particular set of possible outcomes of a probability experiment. Example: A rolled die showing a number less than 3. The experiment is the rolling of the die. The event is {1, 2}.
See also Equally Likely Probability, Experiment, Impossible Probability, Independent Events, Outcome, Probability
Experiment: In probability, an experiment is a procedure used to measure specific instance of outcomes of the experiment. For example, tossing a coin is an experiment, and its possible outcomes are heads and tails.
See also Equally Likely Probability, Event, Impossible Probability, Independent Events, Outcome, Probability
Exponent: The power a number or variable is raised to in an expression. This power can be positive, negative, zero, and fractional. Indeed, the exponent can be any real number. If the exponent is 0, then the value reduces to 1; that is, \(\begin{align}x^0 = 1\end{align}\), for every non-zero real number x. Other examples:
- \(\begin{align}2^3 = 2 \times 2 \times 2 = 8\end{align}\)
- \(\begin{align}2^{-3} = \frac{1}{2^3} = \frac{1}{8}\end{align}\)
- \(\begin{align}2^\frac{1}{2} = \sqrt{2}\end{align}\)
See also Power, Root of a Number
Expression: A combination of algebraic terms that can be used in an equation. Example: \(\begin{align}x^3 + 3x – 4\end{align}\). An expression is not an equation, but can be used as part of an equation.
See also Equation, Equivalent Equations, Independent Equations, Inequality, Linear Equation, Polynomial, Quadratic Equation, Quadratic Formula, Roots of an Equation, Simultaneous Linear Equations, Solutions to an Equation, Unknown Quantity, Variable
Face of a Geometric Solid: A side of a 3-dimensional geometric object. For example, a cube has 6 faces. These can be seen in the figure which also shows the edges and the formula for calculating the cube’s volume.
See also Edge of a Solid Figure, Sides of Geometric Figures, Surface Area, Volume
Factor: A component of a multiplication product. For example, 2 and 3 are factors of 6, since 6 = 2 x 3. Also, the factors of \(\begin{align}x^2 + 5x + 6\end{align}\) are (x + 2) and (x + 3), since (x + 2)(x + 3) = \(\begin{align}x^2 + 5x + 6\end{align}\).
See also Divisible, Divisor, Factorization of Polynomials, Greatest Common Factor (Divisor), Least Common Multiple, Multiple, Prime Factorization, Prime Number, Product, Quotient, Remainder
Factorial: The operation of multiplying a positive integer by every positive integer less than or equal to it. For example, 4 factorial (written 4!) is
\(\begin{align} 4 \times 3 \times 2 \times 1 = 24\end{align}\)
See also Combinations, Permutations
Factorization of Polynomials: An expression which shows a polynomial as a product of two or more smaller polynomials. For example, the following is a factorization of a polynomial:
\(\begin{align} x^2 – 5x + 6 = (x -2)(x – 3)\end{align}\)
The expression on the right of the equals sign is a factorization of the expression on the left.
See also Constant, Coefficient, Variable, Term, Monomial, Product
Fraction: A number, also called a rational number, which is a ratio of two integers, consisting of a numerator and a denominator. 3/4 is a fraction with the numerator being 3 and the denominator being 4.
See also Natural, Integer, Rational, Irrational, Real, Decimal Number, Decimal Point, Percent, Repeating Decimal, Scientific Notation, Denominator, Numerator
Frequency Distribution: A display or mathematical function which shows how many times, or the frequency with which, a variable has each of the values it takes on. For example, suppose Jane sells this number of insurance policies each week in a 10 week period:
1, 3, 1, 4, 5, 3, 2, 1, 1, 2
Then the frequency distribution of these numbers is shown in this table:
| Number of Policies Sold | Frequency |
| 1 | 4 |
| 2 | 2 |
| 3 | 2 |
| 4 | 1 |
| 5 | 1 |
See also Arithmetic Mean, Average, Mean, Median, Mode, Standard Deviation, Statistical Function
Function: A mathematical rule that associates every element in one set – called the domain of the function – with a unique element in some other (or possibly the same) set, called the range. For example, if the function named f is defined by the polynomial 3x + 1, then both the domain and the range of the function f is the set of real numbers. Thus, if x is any real number, then the function f associates x with the value 3x + 1. This is written as f(x) = 3x + 1. This is said “f of x = 3x + 1.” Different values for x and f(x) are shown in the following table:
| x | f(x) = 3x + 1 |
| 0 | 1 |
| 2 | 7 |
| 3 | 10 |
| -1 | -2 |
| -2 | -5 |
Thus, if x is 0, then f(x) is 1; if x is 2, f(x) is 7, etc. We can shorten this by saying, f(0) = 1, f(2) = 7, etc. Notice that we replace the x in the expression f(x) and in the polynomial 3x + 1 with the number 0 or the number 2, etc., so, for example, f(2) = 3·2 + 1 = 6 + 1 = 7.
See also Domain of a Function, Range of a Function
Geometry Word Problem: A word problem which involves using concepts and facts from geometry for its solution. These might include, for example, calculating areas or volumes, or using the Pythagorean theorem to determine a distance.
See also Data Interpretation Problem, Discount/Markup Word Problem, Interest Word Problem, Measurement Word Problem, Mixture Word Problem, Profit Word Problem, Rate Word Problem, Set Word Problem, Word Problem, Work Word Problem
Greatest Common Factor (Divisor): The largest number which evenly divides two or more numbers. The greatest common factor (or the greatest common divisor) of 20 and 24, for example, is 4. Even though 2 evenly divides both numbers, it’s smaller than 4, so 4 is the greatest common factor.
See also Prime Factorization, Least Common Multiple, Factorial
See also Parallelogram, Pentagon, Polygon, Quadrilateral, Rectangle, Square, Trapezoid, Triangle
Hypotenuse: The side of a right triangle opposite the right angle. The figure shows a right triangle with the side marked ‘C’ as the hypotenuse.
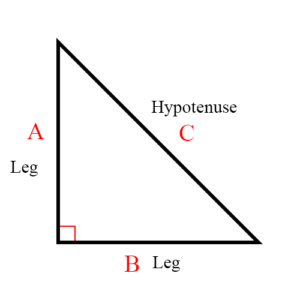 See also Right Triangle, Legs, Pythagorean Theorem
See also Right Triangle, Legs, Pythagorean Theorem
Impossible Probability: This is a probability of 0. If an event cannot happen, then its probability is 0. Conversely, if the probability of an event is 0, then the event cannot happen.
See also Equally Likely Probability, Event, Experiment, Independent Events, Outcome, Probability
Improper Fraction: A fraction whose numerator is larger than its denominator. Example: 3/2
See also Fraction
Independent Equations: Multiple equations that are not equivalent.
See also Equation, Equivalent Equations, Expression, Inequality, Linear Equation, Polynomial, Quadratic Equation, Quadratic Formula, Roots of an Equation, Simultaneous Linear Equations, Solutions to an Equation, Unknown Quantity, Variable
Independent Events: Two events are independent if the occurrence of one doesn’t affect the probability of the other. For example, if the probability that a person will be born in January is .1 and in July is .15, then if John is born in January, this doesn’t change the probability that Mary is born in July or in January or in any other month. The two events are independent, so the occurrence of one doesn’t change the probability of the occurrence of the other. Tosses of coins and rolls of dice are also independent events. If a coin toss comes up heads 20 times in a row, then the probability it will come up heads the 21st time is still 1/2, because the tosses are independent.
See also Equally Likely Probability, Event, Experiment, Impossible Probability, Outcome, Probability
Inequality: A mathematical statement that two quantities are comparable but not necessarily equal. Usually, it includes an indication as to which quantity is greater or less. For example: x ≤ 3, says x can be 3, but it might be less than 3. As a second example, x < 3 says x is definitely less than 3. Inequalities are expressed using the following operators: <, >, ≤, ≥, ≠.
Inequalities are solved just as equations are, with one notable exception. In an inequality, if you multiply or divide both sides by the same negative number, then you reverse the direction of the inequality.
See also Absolute Value, Equation, Equivalent Equations, Expression, Independent Equations, Linear Equation, Polynomial, Quadratic Equation, Quadratic Formula, Roots of an Equation, Simultaneous Linear Equations, Solutions to an Equation, Unknown Quantity, Variable
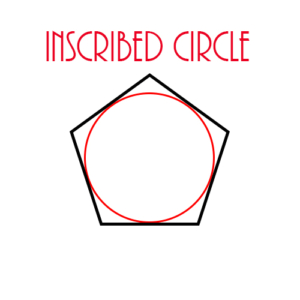
Inscribed Circle: A circle within a polygon that is tangent to all sides of the polygon.
See also Circle, Circumscribed Circle, Circumscribed Polygon, Inscribed Polygon, Center, Radius, Diameter, Circumference, Tangent, Secant
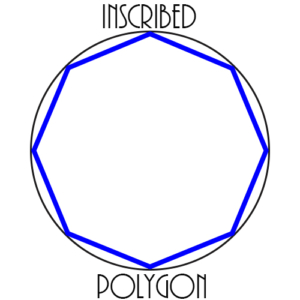
Inscribed Polygon: A polygon inside a circle in which every vertex of the polygon is on the circle. In this case, the circle is circumscribed around the polygon, as shown in the figure.
See also Circle, Circumscribed Circle, Circumscribed Polygon, Inscribed Circle, Center, Radius, Diameter, Circumference, Tangent, Secant
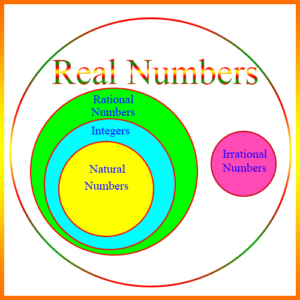
Integer: A whole number, which can be positive, negative, or zero. For example, 5, 17, -8, -365, and 0 are integers. The figure shows the subset relationships of the real numbers, with the integers as a subset of the rational numbers.
See also Natural, Rational, Fraction, Irrational, Real
Intercept: The point at which a line passes through the x- or the y-axis. At the y-intercept, the x coordinate for the point will be 0, and at the x-intercept the y coordinate will be 0. For example, in the equation, as shown in the figure:
\(\begin{align}y = 3x + 12\end{align}\)
the line passes through the y-axis at y = 12, and through the x-axis as x = -4. Thus, the y-intercept is 12 and the x-intercept is -4.
See also Coordinate Axes, Coordinates, Quadrants, Point, Line, Slope
Interest Word Problem: A word problem involving interest rates or amounts. Example: If $100 is invested at 4% interest compounded annually, what is the amount it grows to in 2 years? Answer: $108.16
See also Data Interpretation Problem, Discount/Markup Word Problem, Geometry Word Problem, Measurement Word Problem, Mixture Word Problem, Profit Word Problem, Rate Word Problem, Set Word Problem, Word Problem, Work Word Problem
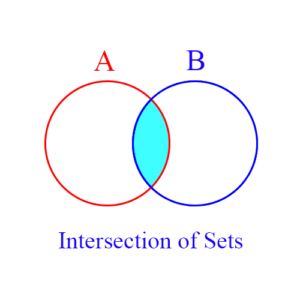
Intersection of Sets: The intersection of two sets is itself a new set, and consists of those elements that are in both sets. For example, suppose A = {1, 2, 3} and B = {2, 3, 4}, then the intersection of A and B is {2, 3} – written A ∩ B = {2, 3}. The blue shaded area in the figure represents the intersection of sets A and B.
See also Cardinality of a Set, Difference of Sets, Disjoint Sets, Element of a Set, Empty Set, Set, Set Word Problem, Union of Sets, Venn Diagram
Inverse: The inverse of a number x is a number which when multiplied by x yields 1 as the product. Example: The inverse of 2 is 1/2, because 2 × 1/2 = 1. Also, the inverse of 3/4 is 4/3; the inverse of 1 is 1; and the inverse of -1 is -1. The inverse is often called the reciprocal because the inverse of a fraction is the fraction inverted, as in 3/4 is the inverse of 4/3, and 4/3 is the inverse of 3/4. The only number without an inverse is 0, because division by 0 is undefined, so 0 has no reciprocal.
See also Fraction, Reciprocal
Irrational Number: A number which is a real number, but is not a rational number. That is, it cannot be expressed as a ratio of two integers. \(\begin{align} \sqrt{2}\end{align}\) and \(\begin{align}\pi\end{align}\) are irrational numbers. The figure shows the irrational numbers as a subset of the set of real numbers.
See also Natural, Integer, Rational, Fraction, Real
Isosceles Triangle: A triangle with two equal sides. The two angles opposite the two equal sides will also be equal.
See also Acute, Right, Equilateral, Scalene, Obtuse, Similar, Congruent
Least Common Multiple (lcm): The smallest positive integer which is a multiple of two or more integers. For example, the least common multiple of 6 and 10 is 30, since even though 60 is a multiple of both numbers, 30 is also and is smaller than 60.
See also Prime Factorization, Greatest Common Factor (Divisor), Factorial
Legs of a Right Triangle: The two sides of the right triangle whose intersection forms the right angle. The figure shows a right triangle in which A and B are its legs.
See also Right Triangle, Hypotenuse, Pythagorean Theorem
Line: A set of points on the coordinate plane that is defined by a linear equation with x and y as variables. Every pair of (x, y) points that satisfies the equation is on the line, and every pair that does not satisfy the equation is not on the line. An example of such an equation is
\(\begin{align}y = 3x + 5\end{align}\)
This equation defines a straight line which passes through the y axis at y = 5.
See also Coordinate Axes, Coordinates, Quadrants, Point, Slope, Intercept
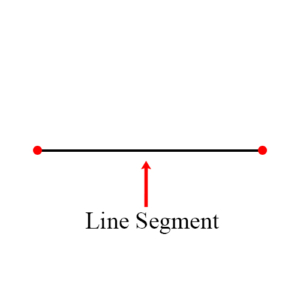
Line Segment: A finite portion of a line between two endpoints.
See also Endpoints of a Line Segment
Linear Equation: An equation with x, or x and y, as variables, but with every variable having an exponent of 1. Examples:
\(\begin{align}4x + 2 = 6\end{align}\)
\(\begin{align}5x – 3y = 17\end{align}\)
They are called “linear” because the graph of such an equation on the coordinate plane is a straight line.
See also Equation, Equivalent Equations, Expression, Independent Equations, Inequality, Polynomial, Quadratic Equation, Quadratic Formula, Roots of an Equation, Simultaneous Linear Equations, Solutions to an Equation, Unknown Quantity, Variable
Mean: The computed average of a list of numbers. For example, the mean of a list of 3 numbers is calculated by adding the 3 numbers together and then dividing by 3.
See also Arithmetic Mean, Average, Frequency Distribution, Median, Mode, Standard Deviation, Statistical Function
Measurement Word Problem: A word problem involving distances, rates, quantities, etc., given in either the metric or the English measurement system.
See also Data Interpretation Problem, Discount/Markup Word Problem, Geometry Word Problem, Interest Word Problem, Mixture Word Problem, Profit Word Problem, Rate Word Problem, Set Word Problem, Word Problem, Work Word Problem
Median: The number whose value is in the middle of the values of a list of numbers. Example: In the list, 8, 15, 6, 9, 14, the median is 9, since its value is less than 14 and 15, and greater than 6 and 8.
See also Arithmetic Mean, Average, Mean, Frequency Distribution, Mode, Standard Deviation, Statistical Function
Mixture Word Problem: A word problem that involves different types of solutions or substances being mixed together. Typically, the problem is some variation of taking a solution with a certain percentage of some substance in it and mixing it with another solution with a different percentage of the same substance and determining what the percentage of the substance is in the new solution.
See also Data Interpretation Problem, Discount/Markup Word Problem, Geometry Word Problem, Interest Word Problem, Measurement Word Problem, Profit Word Problem, Rate Word Problem, Set Word Problem, Word Problem, Work Word Problem
Mode: The value in a list of values that occurs the most frequently. Thus, if we have a list, 3, 8, 8, 4, 7, then the mode is 8.
See also Arithmetic Mean, Average, Mean, Median, Frequency Distribution, Standard Deviation, Statistical Function
Monomial: A polynomial with only a single term. Example: \(\begin{align}3x^2\end{align}\)
See also Constant, Coefficient, Variable, Term, Product, Factorization
Multiple: An integer a is a multiple of b if there is some integer n, such that a = bn.
See also Divisible, Divisor, Factor, Factorization of Polynomials, Greatest Common Factor (Divisor), Least Common Multiple, Prime Factorization, Prime Number, Product, Quotient, Remainder
Mutually Exclusive Sets: These are sets which are disjoint, as shown in the figure below. That is, they have no elements in common. If A and B are mutually exclusive, then A ∩ B = ∅.
See also Disjoint Sets
Natural Number: A positive integer, or “counting number.” 1, 2, 3, etc. are natural numbers. 0 is sometimes considered a natural number also. The figure shows the natural numbers as a subset of the integers.
See also Integer, Rational, Fraction, Irrational, Real
Numerator: The top number in a fraction. Example: In the fraction 3/4, 3 is the numerator.
See also Denominator, Fraction
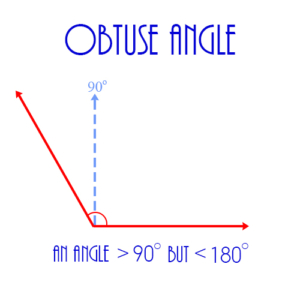
Obtuse Angle: An angle larger than 90 degrees but less than 180 degrees.
See also Acute, Right, Vertical, Complementary, Supplementary Angles
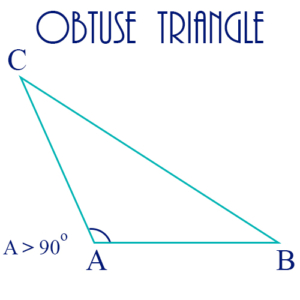
Obtuse Triangle: A triangle with one obtuse angle.
See also Acute, Right, Equilateral, Isosceles, Scalene, Similar, Congruent
Odd Integer: An integer which is not evenly divisible by 2. Examples: 1, 3, 5, 7.
See also Consecutive Even Integers, Consecutive Integers, Consecutive Odd Integers, Divisible, Divisor, Even Integer, Integer, Multiple, Quotient, Remainder
Origin: The point (0, 0) on the coordinate plane. In the figure the origin is the point at which the vertical or y-axis and the horizontal or x-axis cross.
See also Point on the Coordinate Plane, Coordinate Axes, Coordinates, x-axis, x-coordinate, x-intercept, y-axis, y-coordinate, y-intercept
Outcome: A possible result of a probability experiment. Examples: In the probability experiment of tossing a coin, the possible outcomes are heads and tails. In the probability experiment of rolling a die, the possible outcomes are the numbers 1 – 6.
See also Equally Likely Probability, Event, Experiment, Impossible Probability, Independent Events, Probability
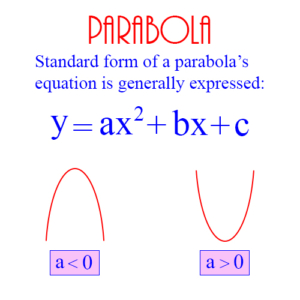
Parabola: A geometric figure which results by graphing a quadratic formula on the coordinate plane. The figure below shows the general form of the quadratic expression which defines the parabola. Note that if a is less than 0 the parabola rises to a maximum point, whereas if a is positive the parabola goes down to a minimum point.
See also Coordinate Axes, Coordinates, Line, Quadrants, Point, Slope, Intercept
Parallel Lines: Two lines in the same plane which never intersect.
See also Line, Perpendicular, Transversal, Tangent, Secant,
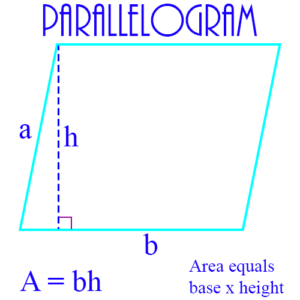
Parallelogram: A 4-sided geometric figure in which opposite sides are parallel.
See also Hexagon, Pentagon, Polygon, Quadrilateral, Rectangle, Square, Trapezoid, Triangle
Pentagon: A 5-sided polygon.
See also Hexagon, Parallelogram, Polygon, Quadrilateral, Rectangle, Square, Trapezoid, Triangle
Percent: A fraction expressed in 100th’s, in which only the numerator is written, and the denominator is assumed to be 100. Example: 50 percent (written 50%) actually means 50/100.
See also Decimal Number, Decimal Point, Fraction, Rational Number, Repeating Decimal, Scientific Notation
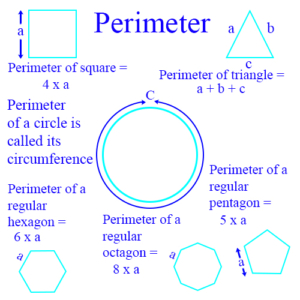
Perimeter: The distance around a geometric figure, usually a polygon. (The perimeter of a circle is called its circumference.) Example: The perimeter of a rectangle is the sum of the lengths of its 4 sides. If l is the length of the rectangle, and w is its width, then the perimeter p is calculated by p = 2l + 2w. The figure below shows perimeters of several polygons, as well as the perimeter or circumference of a circle.
See also Polygon, Hexagon, Parallelogram, Pentagon, Quadrilateral, Rectangle, Square, Trapezoid, Triangle
Permutations: Different arrangements of a set of objects, where order is important. For example, {1, 2, 3} can be ordered in 6 different ways: 123, 132, 213, 231, 312, 321. The number of permutations of a set of n objects is n! (n factorial)
See also Combinations, Probability, Factorial
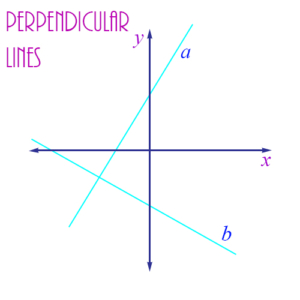
Perpendicular Lines: Two lines which intersect at a right angle. In the figure, the lines a and b are perpendicular.
See also Line, Parallel, Transversal, Tangent, Secant, Right Angle
Point of Tangency: The single point on a circle and a tangent line where the circle and the tangent line meet. In the figure the point of tangency is where the tangent line and the radius shown intersect.
See also Tangent, Line, Radius, Diameter, Circumference, Secant, Circle
Point on the Coordinate Plane: A place on the coordinate plane which is exactly identified by two real numbers, the x-coordinate and the y-coordinate of the point. The figure shows a point on the plane with coordinates (-3, 4). It is the center of a circle.
Other examples:
-
-
-
-
- (4, 3) is the point 4 units to the right on the x-axis, and 3 units up on the y-axis. It’s in the first quadrant.
- (-4, 3) is the point 4 units to the left on the x-axis, and 3 units up on the y-axis. It’s in the second quadrant.
- (-4, -3) is the point 4 units to the left on the x-axis, and 3 units down on the y-axis. It’s in the third quadrant.
- (4, -3) is the point 4 units to the right on the x-axis, and 3 units down on the y-axis. It’s in the fourth quadrant.
- (0, 0) is the origin. It is not in any quadrant, but is the point where the x and y axes intersect.
-
-
-
See also Coordinate Axes, Coordinates, Origin, Quadrants, Line, Slope, Intercept
Polygon: A closed geometric figure consisting of connected line segments. If all its angles are less than 180°, then it is convex. Examples: Triangles, squares, rectangles, pentagons, hexagons. The figure shows an example of a hexagon.
See also Hexagon, Parallelogram, Pentagon, Quadrilateral, Rectangle, Square, Trapezoid, Triangle
Polynomial: An algebraic expression consisting of multiple terms connected by plus (+) or minus (-) signs. Example: \(\begin{align}x^3 + 3x – 4\end{align}\)
See also Equation, Expression, Inequality, Linear Equation, Monomial, Quadratic Equation, Quadratic Formula, Roots of an Equation, Simultaneous Linear Equations, Solutions to an Equation, Term, Unknown Quantity, Variable
Power: An exponent given to a number or variable showing how many times the number (variable) is included in a product. Example: 4² = 4·4 = 16. In this example, 4 is said to be “raised” to the power of 2.
See also Exponent, Root of a Number
Prime Factorization: The representation of a positive integer as a product of powers of primes. For example, the prime factorization of 180 is
\(\begin{align} 2^2 \times 3^2 \times 5\end{align}\)
since the only prime numbers that divide 180 are 2 (twice), 3 (twice), and 5.
See also Factor, Prime Number, Least Common Multiple, Greatest Common Factor (Divisor)
Prime Number: An integer greater than 1 which can only be evenly divided by itself or by 1. Examples: 2, 3, 5, 17, 43.
See also Divisible, Divisor, Factor, Factorization of Polynomials, Greatest Common Factor (Divisor), Least Common Multiple, Multiple, Prime Factorization, Product, Quotient, Remainder
Probability: A number between 0 and 1 which represents the likelihood of a certain event’s happening. It’s typically measured as a fraction, with the number of possible outcomes of the event in the denominator, and the number of favorable events in the numerator. For example, if you randomly draw a card from a pack of 52 with 4 aces in it, the probability of drawing an ace is 4/52, or 1/13.
See also Combinations, Conditional Probability, Permutations, Factorial, Equally Likely Probability, Event, Experiment, Impossible Probability, Independent Events, Outcome
Product: The result of the multiplication of 2 or more factors of a polynomial, or two or more numbers otherwise. Example of a polynomial product:
\(\begin{align} (x + 2) (x – 4) = x^2 – 2x – 8\end{align}\)
See also Constant, Coefficient, Variable, Term, Monomial, Factorization
Profit Word Problem: A word problem dealing with the values of revenue and cost in a commercial organization. Profit = Revenue – Cost.
See also Data Interpretation Problem, Discount/Markup Word Problem, Geometry Word Problem, Interest Word Problem, Measurement Word Problem, Mixture Word Problem, Rate Word Problem, Set Word Problem, Word Problem, Work Word Problem
Proportion: A statement of equality between two fractions or ratios. Thus, a proportion problem might be x/2 = 8/4, for which x = 4.
See also Fraction, Denominator, Numerator
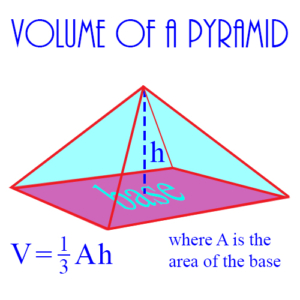
Pyramid: A 3-dimensional object, with a base which is usually a square or an equilateral triangle, and each vertex of which is connected via a straight line to an apex. The figure shows a pyramid with a rectangular base, as well as the formula for calculating its volume.
See also Base of a Cylinder, Cone, Cube, Cylinder, Sphere
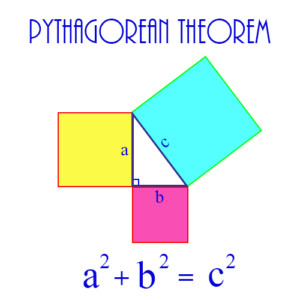
Pythagorean Theorem: A statement that shows the relationship between the hypotenuse and the legs of a right triangle as a famous formula:
\(\begin{align}a^2 + b^2 = c^2\end{align}\)
where a and b are the lengths of the legs of the triangle, and c is the length of the hypotenuse.
See also Right Triangle, Hypotenuse, Legs, Acute, Equilateral, Isosceles, Scalene, Obtuse, Similar, Congruent
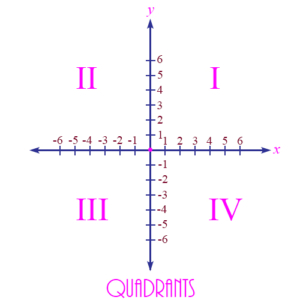
Quadrants: The four sections of the coordinate plane – the first quadrant is the upper right, the second is the upper left, the third is the lower left, and the fourth is the lower right. A point in any of the quadrants will have positive or negative coordinates as follows: Quadrant I: x positive, y positive; Quadrant II: x negative, y positive; Quadrant III: x negative, y negative; Quadrant IV: x positive, y negative. Points on the two axes do not lie in any quadrant.
See also Coordinate Axes, Coordinates, Point, Origin, Line, Slope, Intercept
Quadratic Equation: A polynomial equation with x as the only variable, and where the highest power of x is 2. Examples:
- \(\begin{align}x^2 + 4x – 5 = 0\end{align}\)
- \(\begin{align}3x^2 +2x – 15 = 0\end{align}\)
All quadratic equations can be solved using the quadratic formula.
See also Equation, Equivalent Equations, Expression, Independent Equations, Inequality, Linear Equation, Polynomial, Quadratic Formula, Roots of an Equation, Simultaneous Linear Equations, Solutions to an Equation, Unknown Quantity, Variable
Quadratic Formula: This is a general formula that can be used to solve any quadratic equation.
\(\begin{align} x = \frac { – b \pm \sqrt {b^2 – 4ac} } {{2a}}\end{align}\)
where the original equation has the form:
\(\begin{align}ax^2 + bx + c = 0\end{align}\)
If the portion under the square root sign, b² – 4ac, is greater than or equal to 0, then the roots of the equation will be real numbers. Otherwise, they will be complex or imaginary numbers.
See also Equation, Equivalent Equations, Expression, Independent Equations, Inequality, Linear Equation, Polynomial, Quadratic Equation, Roots of an Equation, Simultaneous Linear Equations, Solutions to an Equation, Unknown Quantity, Variable
Quadrilateral: A 4-sided polygon. Examples: Rectangle, square, parallelogram. The figure shows a rectangle.
See also Hexagon, Parallelogram, Pentagon, Polygon, Rectangle, Square, Trapezoid, Triangle
Quotient: The result of a division operation. It’s possible the operation may yield a remainder as well as a quotient. Thus, if we divide 20 by 3, then the quotient is 6, but there is a remainder of 2.
See also Divisible, Divisor, Factor, Factorization of Polynomials, Greatest Common Factor (Divisor), Least Common Multiple, Multiple, Prime Factorization, Prime Number, Product, Remainder
Radius of a Circle: Any line segment from the center of the circle to a point on the circle. Its length (also called “the radius”) is always half the length of a diameter.
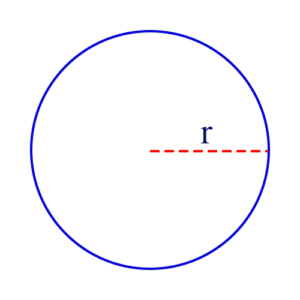
See also Diameter, Circumference, Tangent, Secant, Circle
Range of a Function: A set which provides the set of values for a function. Thus, if f is a function whose domain is the set of real numbers, and f(x) = x², then the range of the function f is the non-negative real numbers.
See also Domain of a Function, Function
Range of a Set of Values: The difference between the lowest and the highest values in a set of values. Example: The set of values -4, -1, 8 has a range of 12, since 8 – (-4) = 8 + 4 = 12.
See also Arithmetic Mean, Average, Frequency Distribution, Mean, Median, Mode, Standard Deviation, Statistical Function
Rate Word Problem: A word problem that typically deals with the formula distance = rate x time, but there can be other types of rate problems as well that deal with linear change. Example: If Billy makes $60,000 per year and his salary is growing by $5000 per year, what will he be making in 3 years?
See also Data Interpretation Problem, Discount/Markup Word Problem, Geometry Word Problem, Interest Word Problem, Measurement Word Problem, Mixture Word Problem, Profit Word Problem, Set Word Problem, Word Problem, Work Word Problem
Ratio: A fractional relationship between 2 numbers. Thus, the ratio of a to b is a/b. It can also be shown as a:b.
See also Fraction
Rational Number: A number which is a fraction or “ratio” between two integers. 2/5, 25/8, -4/3, and 0 are all rational numbers. Every integer is a rational number. Rational numbers are also considered real numbers. The figure shows rational numbers as a subset of real numbers and containing integers and natural numbers as subsets.
See also Natural, Integer, Fraction, Irrational, Real, Decimal Number, Decimal Point, Fraction, Percent, Repeating Decimal, Scientific Notation
Real Number: A number which is either a rational or an irrational number. Notice this division of the two types of real numbers in the figure above.
See also Natural, Integer, Rational, Fraction, Irrational
Reciprocal: The inverse of a number. If a number is multiplied by its reciprocal, then the product is 1. Examples: The reciprocal of 2/3 is 3/2, so 2/3 × 3/2 = 1. The reciprocal of 5 is 1/5, so 5 × 1/5 = 1.
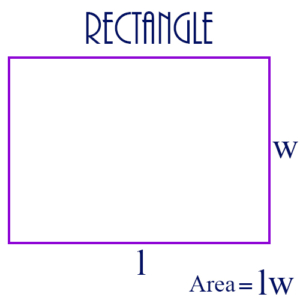
Rectangle: A 4-sided geometric figure with each angle a right angle.
See also Hexagon, Parallelogram, Pentagon, Polygon, Quadrilateral, Square, Trapezoid, Triangle
Rectangular Solid: A 3-dimensional figure with 6 sides, all of which are rectangles. The figure shows an example, together with the formula for calculating its surface area.
See also Cone, Cube, Cylinder, Pyramid, Sphere, Circle,
Remainder: If an integer n is not evenly divisible by another integer k, then we can find integers q and r, such that n = qk + r, where q is maximized, and r < k. The integer q is called the quotient, and r is the remainder. Example: Let n be 25 and k be 7. Then q is 3 and r is 4, because 25 = 3·7 + 4.
See also Divisible, Divisor, Factor, Factorization of Polynomials, Prime Factorization, Prime Number, Product, Quotient
Repeating Decimal: A decimal number which repeats a pattern of integers infinitely. It is always equivalent to some rational number. Example: The infinitely repeating decimal .428571428571428571… is actually the rational number 3/7.
See also Decimal Number, Decimal Point, Fraction, Percent, Rational Number, Scientific Notation
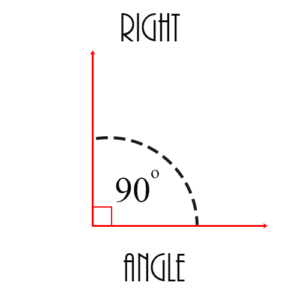
Right Angle: An angle of 90 degrees.
See also Acute, Obtuse, Vertical, Complementary, Supplementary Angles
Right Triangle: A triangle with a right angle.
See also Acute, Equilateral, Isosceles, Scalene, Obtuse, Similar, Congruent, Pythagorean Theorem, Hypotenuse, Legs
Root of a Number: A real number which when raised to the appropriate power yields the original number. Examples: The square root of 2, when multiplied by itself equals 2. The cubed root of 5, when raised to the 3rd power equals 5.
Roots of an Equation: Solutions to an equation. This term is usually used if the roots are solutions to a quadratic equation. Example: Suppose we have the equation \(\begin{align}x^2 – 5x + 6 = 0\end{align}\). Then 2 and 3 are roots of this equation.
See also Equation, Equivalent Equations, Expression, Independent Equations, Inequality, Linear Equation, Polynomial, Quadratic Equation, Quadratic Formula, Simultaneous Linear Equations, Solutions to an Equation, Unknown Quantity, Variable
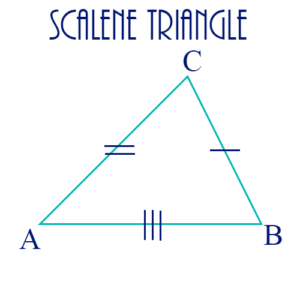
Scalene Triangle: A triangle with 3 unequal sides. The figure shows an acute triangle which is also scalene. An obtuse triangle can also be a scalene triangle.
See also Acute, Right, Equilateral, Isosceles, Obtuse, Similar, Congruent
Scientific Notation: A representation of a decimal or integer as a value between 1 and 10, multiplied by a power of 10. Examples:
\(\begin{align}99999 = 9.9999 \times 10^4\end{align}\)
\(\begin{align}.099 = 9.9 \times 10^{-2}\end{align}\)
The exponent for 10 indicates the number of places the decimal point should be moved to the right or to the left. In the first example above, the exponent is 4, so to get the original number, you move the decimal point 4 places to the right. In the second example, the exponent is -2, so you move the decimal point 2 places to the left.
See also Decimal Number, Decimal Point, Fraction, Percent, Rational Number, Repeating Decimal
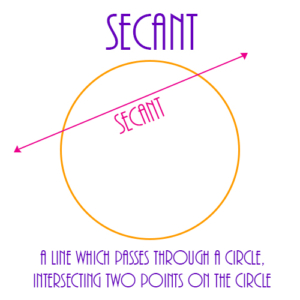
Secant: A line which passes through a circle, intersecting 2 points on the circle.
See also Line, Radius, Diameter, Circumference, Tangent, Circle
Sequence: A series of numbers with the property that each number after the first has a particular relationship to its immediate predecessor. Example: In this sequence, 4, 7, 10, 13, … each number is 3 greater than the number preceding it. This is an example of an arithmetic sequence. The value of each number in a sequence can be determined if we know the value of the first number and the rule that determines for any given number what the next number will be.
A sequence is actually a function whose domain is usually the set of non-negative integers. Its range can vary, but is usually some subset of the real numbers.
See also Domain of a Function, Function
Set: A collection of things. In mathematics sets are usually collections of numbers. Examples of sets: All positive integers, all odd integers, all real numbers, {1, 5, -1, 2}. Set operations include set union, intersection, and difference.
See also Cardinality of a Set, Difference of Sets, Element of a Set, Empty Set, Intersection of Sets, Set Word Problem, Subset, Union of Sets, Venn Diagram
Set Word Problem: A word problem involving the definition of several sets and their possible relationships and operations. Venn diagrams are often useful in the solution of set word problems.
See also Cardinality of a Set, Difference of Sets, Element of a Set, Empty Set, Intersection of Sets, Set, Union of Sets, Venn Diagram, Data Interpretation Problem, Discount/Markup Word Problem, Geometry Word Problem, Interest Word Problem, Measurement Word Problem, Mixture Word Problem, Profit Word Problem, Rate Word Problem, Word Problem, Work Word Problem
Sides of Geometric Figures: In polygons sides are the line segments which together make the polygon. Thus, a hexagon is a 6-sided polygon; a rectangle is a 4-sided polygon. In polyhedrons, 3-dimensional geometric figures, sides are called faces. Thus, a cube has 6 faces.
See also Edge of a Solid Figure, Face of a Geometric Solid, Surface Area, Volume
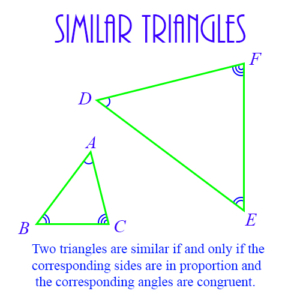
Similar Triangles: Two triangles with corresponding angles equal to each other. Their corresponding sides are in the same ratio, but they aren’t necessarily equal.
See also Acute, Right, Equilateral, Isosceles, Scalene, Obtuse, Congruent
Simultaneous Linear Equations: Multiple linear equations in several variables, each of which has the same value in each equation. If the number of independent linear equations is the same as the number of variables or unknowns in the equations, then the values of the unknowns can be determined. Example:
2x + 6 = 4y
3x – 2 = y + 4
In this system there are 2 equations in 2 unknowns. The solution to the system of equations is x = 3 and y = 3.
See also Equation, Equivalent Equations, Expression, Independent Equations, Inequality, Linear Equation, Polynomial, Quadratic Equation, Quadratic Formula, Roots of an Equation, Solutions to an Equation, Unknown Quantity, Variable
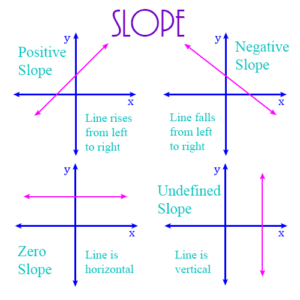
Slope: The rate at which a line is rising or falling. If a line’s slope is positive, then the line is rising as it moves from left to right. If the slope is negative, then the line is falling as it moves from left to right. A simple example is:
\(\begin{align}y = 3x\end{align}\)
This line increases its y value by 3 every time its x value increases by 1. Thus, if x = 0, then y = 0. If x = 1, y = 3, etc. We say in this case that the slope of the line is 3.
For an opposite example, consider:
\(\begin{align}y = -3x\end{align}\)
On this line if x = 0, then y = 0, but if x = 1, then y = -3. So every time x increases by 1, y decreases by 3. So the slope of this line is -3. The figure below shows 4 possible values for a line’s slope: positive, negative, zero, or undefined.
See also Coordinate Axes, Coordinates, Quadrants, Point, Line, Intercept
Slope-Intercept Form: The form of the equation of a line that shows the value of y in terms of x. It is usually given as
\(\begin{align} y = mx + b\end{align}\)
where m is the slope of the line, and b is the value of the y-intercept. Notice that when x is 0, then y = b, so the line crosses the y-axis at b. That is, b is the y-intercept.
See also Line, Linear Equation, Intercept, Slope
Solutions to an Equation: See Roots of an Equation.
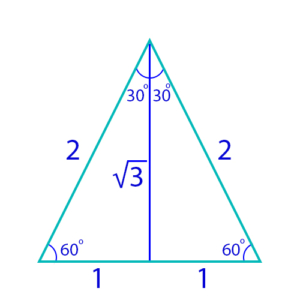
Special Triangles: These triangles occur frequently in problems because of their “natural” structure.
30-60-90: This triangle is one-half of an equilateral triangle. A line from the apex of an equilateral triangle to the midpoint of the base results in two congruent right triangles (see diagram). If each side of the equilateral triangle is of length 2, then the three sides of each half of the triangle have lengths as shown in the diagram.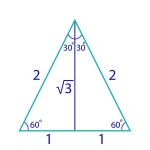
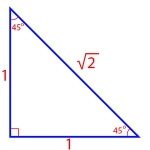
45-45-90: This triangle is an isosceles right triangle. If we assume that the legs of the triangle are each of length 1, then its 3 sides have lengths as shown in the diagram.
See also Acute, Right, Pythagorean Theorem, Legs, Hypotenuse, Equilateral, Isosceles, Scalene, Obtuse, Similar, Congruent
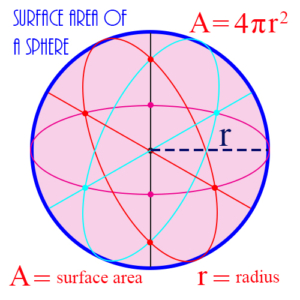
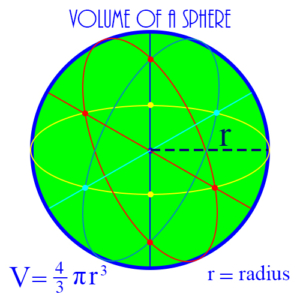
Sphere: A 3-dimensional figure consisting of a set of points, all of which are the same distance from a single, central point. The distance from the center point to any point on the sphere is the radius of the sphere. The figure shows a sphere of radius r, together with the formula for the surface area of the sphere.
See also Base of a Cylinder, Cone, Cube, Cylinder, Pyramid, Circle
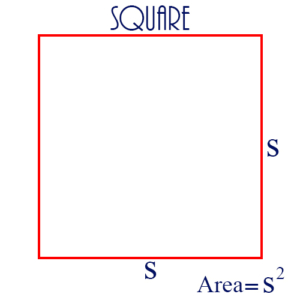
Square: A 4-sided figure with each side the same length and each angle a right angle.
See also Hexagon, Parallelogram, Pentagon, Polygon, Quadrilateral, Rectangle, Trapezoid, Triangle, Right Angle
Square Root: A number which when multiplied by itself yields the number for which it is the square root. Example: 3 is the square root of 9, because 3 × 3 = 9. The square roots of most numbers are not rational numbers. For example, the square roots of 2, 3, 5, 7, etc. are real numbers, but they are not rational numbers.
See also Exponent, Power, Root of a Number
Standard Deviation: A statistical function which is used as a measure of the dispersion of a set of values, the larger (or smaller) the standard deviation, the greater (or the less) the dispersion. It is calculated as follows:
- Find the mean of the set of values.
- Calculate the difference of each number and the mean.
- Square each of these differences.
- Take the average of all the squared differences calculated in step 3.
- Take the square root of the average calculated in step 4.
Example: Suppose the values are 1, 2, 4, 5. Then the mean is 3, and the numbers of steps 2 and 3 are shown in the following table:
| x | x – mean | (x – mean)2 |
| 1 | -2 | 4 |
| 2 | -1 | 1 |
| 4 | 1 | 1 |
| 5 | 2 | 4 |
The average of 4, 1, 1, and 4 is 2.5. The square root of this is approximately 1.58. This is the standard deviation for this sample set to two decimal places.
See also Arithmetic Mean, Average, Frequency Distribution, Mean, Median, Mode, Statistical Function
Statistical Function: A number calculated from a set of values. The particular function is intended to identify something about the set as a whole. Commonly used functions include the mean, median, mode, range, variance, and standard deviation.
See also Arithmetic Mean, Average, Frequency Distribution, Mean, Median, Mode, Standard Deviation, Variance
Subset: A set whose elements are all elements of another set. Thus, if A = {1, 2, 3} and B = {1, 3}, then B is a subset of A, written B ⊂ A. Other important subsets are: The rational numbers are a subset of the real numbers. The integers are a subset of the rational numbers.
See also Cardinality of a Set, Difference of Sets, Element of a Set, Empty Set, Intersection of Sets, Set Word Problem, Union of Sets, Venn Diagram
Supplementary Angles: Two angles whose sum is 180 degrees. In the figure angles 1 and 2 are supplementary, as are angles 1 and 4, 2 and 3, and 3 and 4.
See also Acute, Right, Obtuse, Vertical, Complementary Angles
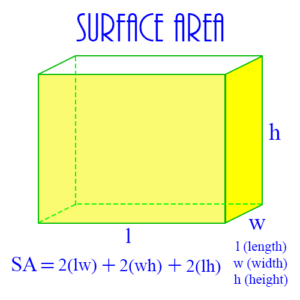
Surface Area: The external area of a 3 dimensional geometric object.
See also Edge of a Solid Figure, Face of a Geometric Solid, Sides of Geometric Figures, Volume
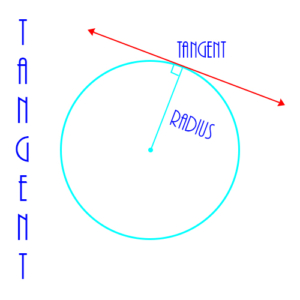
Tangent: A line which intersects or “touches on” a circle at exactly one point.
See also Line, Radius, Diameter, Circumference, Secant, Circle
Term: A single part of a polynomial, consisting of a variable raised to a positive integer power multiplied by a constant, or a single constant with no variable. Also called a monomial. Example:
\(\begin{align} 3x^2 + 5x – 9\end{align}\)
is a polynomial with three terms: \(\begin{align} 3x^2, 5x, -9\end{align}\)
See also Constant, Coefficient, Variable, Monomial, Product, Factorization
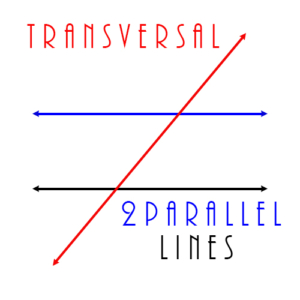
Transversal: A line which intersects two other lines. If the other two lines are parallel, then the transversal makes the same angle with both of them.
See also Line, Parallel, Perpendicular, Tangent, Secant
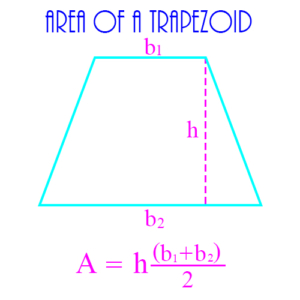
Trapezoid: A 4-sided figure with two opposite sides parallel, but whose other two opposite sides are not parallel. The figure shows a trapezoid together with the formula for its area.
See also Hexagon, Parallelogram, Pentagon, Polygon, Quadrilateral, Rectangle, Square, Triangle
Triangle: A 3-sided polygon. The figure shows a triangle, together with the formula for its area.
See also Hexagon, Parallelogram, Pentagon, Polygon, Quadrilateral, Rectangle, Square, Trapezoid, Equilateral Triangle, Isosceles Triangle, Right Triangle, Special Triangles
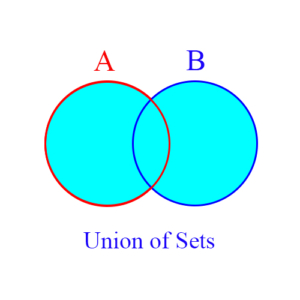
Union of Sets: A set operation which from 2 existing sets creates a new set consisting of all elements that are in either or both of the original sets. Example: If A = {1, 2, 3} and B = {2, 3, 4, 5}, then the set union of A and B, written A ∪ B, is {1, 2, 3, 4, 5}.
See also Cardinality of a Set, Difference of Sets, Element of a Set, Empty Set, Intersection of Sets, Set, Set Word Problem, Venn Diagram
Unknown Quantity: The variable in an equation which can be solved to determine the value of the unknown. For example: In the equation 2x + 5 = 9, x is the unknown, and its value is 2.
See also Equation, Equivalent Equations, Expression, Independent Equations, Inequality, Linear Equation, Polynomial, Quadratic Equation, Quadratic Formula, Roots of an Equation, Simultaneous Linear Equations, Solutions to an Equation, Variable
Variable: A symbol in a polynomial, usually a letter from the end of the alphabet like x, y, or z, which may represent any number from a set, usually the set of real numbers. Example: In the polynomial
\(\begin{align} 3x^2 + 5x – 9\end{align}\)x is a variable, and 3 and 5 are coefficients. -9 is a constant term.
See also Constant, Coefficient, Equation, Term, Monomial, Product, Factorization, Unknown Quantity
Variance: A statistical function which provides a measure of the distribution of a set of data values. It’s calculated by taking the square of the difference of each value and the mean, and then taking the average of these values. The square root of the variance is the standard deviation.
See also Arithmetic Mean, Average, Frequency Distribution, Mean, Median, Mode, Standard Deviation
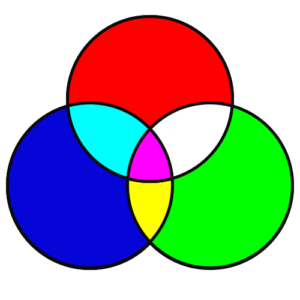
Venn Diagram: A pictorial representation of sets, usually with circles or rectangles, which shows the relationships between them, including possibly how they overlap or intersect. The figure below shows 3 sets as circles, and shows their intersections. The maroon portion in the center shows the intersection of all 3 sets.
See also Cardinality of a Set, Difference of Sets, Element of a Set, Empty Set, Intersection of Sets, Set, Set Word Problem
Vertex: The point of intersection of two sides of a polygon. In the figure the points A, D, and C are vertices of the larger triangle.
See also Hexagon, Parallelogram, Pentagon, Polygon, Quadrilateral, Rectangle, Square, Trapezoid, Triangle
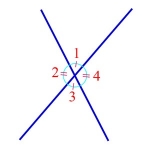
Vertical Angles: Two angles, as angles 1 and 3 in the figure, which are on opposite sides of the intersection of 2 lines.
They are always equal to each other, because they are both supplementary to the same angle. For example, in the figure, angles 1 and 3 are vertical angles and are equal because they’re both supplementary to angle 2. Angles 2 and 4 are also vertical angles and are equal.
See also Acute, Right, Obtuse, Complementary, Supplementary Angles
Volume: The measure of the interior capacity of a 3-dimensional geometric object. Example: The volume of a sphere is 4/3 πr³, where r is the radius of the sphere.
See also Edge of a Solid Figure, Face of a Geometric Solid, Sides of Geometric Figures, Surface Area
Word Problem: A problem in a “real world” situation which can be solved through the application of mathematical concepts. Examples include interest and profit problems, measurement problems, mixture problems, geometry problems, etc.
See also Data Interpretation Problem, Discount/Markup Word Problem, Geometry Word Problem, Interest Word Problem, Measurement Word Problem, Mixture Word Problem, Profit Word Problem, Rate Word Problem, Set Word Problem, Work Word Problem
Work Word Problem: A word problem typically dealing with the length of time it takes to complete a particular task, given that the various workers or machines work at different rates.
See also Data Interpretation Problem, Discount/Markup Word Problem, Geometry Word Problem, Interest Word Problem, Measurement Word Problem, Mixture Word Problem, Profit Word Problem, Rate Word Problem, Set Word Problem, Word Problem
x-axis: The horizontal line used on the coordinate plane to identify the horizontal distance of points from the y-axis.
See also Coordinate Axes, Coordinates, Origin, Quadrants, Point on the Coordinate Plane, Line, Slope, Intercept, x-coordinate, x-intercept, y-axis, y-coordinate, y-intercept
x-coordinate: The first of two numbers which together identify the location of a point on the coordinate plane. The x-coordinate identifies the horizontal distance and direction of the point from the y-axis. If the x-coordinate is positive, then the point is to the right of the y-axis. If negative, the point is to the left. Examples: (2, 3) has x-coordinate 2, which means that the point is 2 units to the right of the y-axis. (-4, 5) has x-coordinate -4, which means the point is 4 units to the left of the y-axis.
See also Coordinate Axes, Coordinates, Origin, Quadrants, Point on the Coordinate Plane, Line, Slope, Intercept, x-axis, x-intercept, y-axis, y-coordinate, y-intercept
x-intercept: The point at which a straight line crosses the x-axis. In the figure below, the x-intercept is -4.
See also Coordinate Axes, Coordinates, Origin, Quadrants, Point on the Coordinate Plane, Line, Slope, Intercept, x-axis, x-coordinate, y-axis, y-coordinate, y-intercept
y-axis: The vertical line used on the coordinate plane to identify the vertical distance of points from the x-axis.
See also Coordinate Axes, Coordinates, Origin, Quadrants, Point on the Coordinate Plane, Line, Slope, Intercept, x-axis, x-coordinate, x-intercept, y-coordinate, y-intercept
y-coordinate: The second of two numbers which together identify the location of a point on the coordinate plane. The y-coordinate identifies the vertical distance and direction of the point from the x-axis. If the y-coordinate is positive, then the point is above the x-axis. If negative, the point is below. Examples: (2, 3) has y-coordinate 3, which means that the point is 3 units above the x-axis. (-4, -5) has y-coordinate -5, which means the point is 5 units below the x-axis.
See also Coordinate Axes, Coordinates, Origin, Quadrants, Point on the Coordinate Plane, Line, Slope, Intercept, x-axis, x-coordinate, x-intercept, y-axis,y-intercept
y-intercept: The point at which a straight line crosses the y-axis. In the figure below, the y-intercept is 5.
See also Coordinate Axes, Coordinates, Origin, Quadrants, Point on the Coordinate Plane, Line, Slope, Intercept, x-axis, x-coordinate, x-intercept, y-axis, y-coordinate