Expressions/Equations
Every Data Sufficiency (DS) question can have 1 of 5 possible answers, and the possible answers are the same for every DS question. All DS questions are really two questions in one. You’re given a general problem, followed by two supplemental statements. The real problem is to evaluate each of the two statements independently to determine their individual sufficiency to solve the original general problem. As you determine the sufficiency of these statements, you are able to decide which of the following 5 answers to the Data Sufficiency question is the correct answer:
A. Statement 1 is sufficient, but statement 2 is not.
B. Statement 1 is not sufficient, but statement 2 is.
C. Neither statement 1 nor statement 2 is sufficient, but together they are.
D. Both statement 1 and statement 2 are individually sufficient.
E. Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
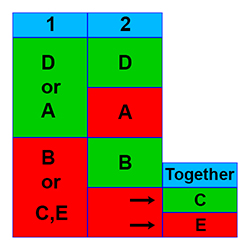
The diagram above gives a pictorial representation of the 5 Data Sufficiency answers. The two statement numbers are shown in blue at the top of the first two columns. Note that green means sufficient, and red means not sufficient. As an example, if both statements 1 and 2 are individually sufficient, then the correct answer is D. For more information on the 5 DS answers, see our videos.
We illustrate these answers for expression/equation problems with the following 11 examples. Each of the first three examples provides 5 different versions of supplementary statements for the same general problem, and each of these 5 versions yields a different one of the 5 possible answers. The answers to these 5 versions are explained immediately after the problem. After the first 3 examples, we then give 8 additional examples with just one version of the supplementary statements.
[Notice in the first 3 examples that the 5 versions of the supplementary statements provide examples of the 5 different answers, A – E. However, they are not given in A – E order.]
Example 1)
Each day Hector is adding money to his checking account and writing checks on the account. How much will he have increased or decreased his account in a 4 day period?
Version I.
(1) He started with $800 in the account.
(2) On average he deposits $89 per day.
Version II.
(1) The average daily difference between deposits and total expenditures is positive $28.
(2) He started with $800 in the account.
Version III.
(1) After 4 days the amount in his account is 14% higher than the $800 he started with.
(2) On average he deposits $89 per day and spends $122 every two days.
Version IV.
(1) He started with $800 in the account.
(2) After 4 days the amount in his account is 14% higher than at the start.
Version V.
(1) After 4 days the amount in his account is 14% higher than at the start.
(2) On average he deposits $89 per day and spends $122 every two days.
Answers: [ Version I: E Version II: A Version III: D Version IV: C Version V: B ]
Explanation:
This problem is straightforward. We simply need to know how much Hector deposits and how much he withdraws over the 4 day period – or equivalent information – to calculate the net result.
Version I: Answer E – Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
(1) He started with $800 in the account.
Partial information. This gives us a starting dollar amount but we need the change in the account. Not sufficient.
(2) On average he deposits $89 per day.
Partial information. We need withdrawals as well as deposits. Not sufficient.
Alone, these two statements are not sufficient, nor are they together, because even though we have a starting amount and a daily deposit average, we have nothing about expenditures.
Version II: Answer A – Statement 1 is sufficient, but statement 2 is not.
(1) The average daily difference between deposits and total expenditures is positive $28.
Full information. Multiply the $28 by 4, and we have the desired result. Sufficient.
(2) He started with $800 in the account.
Partial information. We need the amount the account changed, not how much it started with. Not sufficient.
Version III: Answer D – Both statement 1 and statement 2 are individually sufficient.
(1) After 4 days the amount in his account is 14% higher than the $800 he started with.
Full information. This statement gives us an actual dollar amount at the start and the percent change so we can calculate the actual change. Sufficient.
(2) On average he deposits $89 per day and spends $122 every two days.
Full information. From this we can calculate that he spends $61 per day, and so the net per day is a positive $28. Multiply by 4, and we have the desired result. Sufficient.
Version IV: Answer C – Neither statement 1 nor statement 2 is sufficient, but together they are.
(1) He started with $800 in the account.
Partial information. This gives us an actual dollar amount, but we need the change over the 4 day period, not the amount he started with. Not sufficient.
(2) After 4 days the amount in his account is 14% higher than at the start.
Partial information. This gives us the percent change, but without an actual dollar amount we can’t calculate the needed result. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because knowing the amount he started with and the percent increase we can calculate the dollar increase, which is the desired result.
Version V: Answer B – Statement 1 is not sufficient, but statement 2 is.
(1) After 4 days the amount in his account is 14% higher than at the start.
Partial information. This gives us the percent change, but without an actual dollar amount we can’t calculate the needed result. Not sufficient.
(2) On average he deposits $89 per day and spends $122 every two days.
Full information. From this we can calculate that he spends $61 per day, and so the net per day is a positive $28. Multiply by 4, and we have the desired result. Sufficient.
To practice more problems like this, click here.
Example 2)
Is (a + 1)(b + 1) = 0?
Version I.
(1) -10 ≤ a ≤ 20
(2) a = -(2 + a)
Version II.
(1) ab + 1 = -(a + b)
(2) b > -10
Version III.
(1) -10 ≤ a ≤ 20
(2) b > -10
Version IV.
(1) b = a + 2
(2) b + 1 = 2
Version V.
(1) a = -(2 + a)
(2) ab + 1 = -(a + b)
Answers: [ Version I: B Version II: A Version III: E Version IV: C Version V: D ]
Explanation:
A product of two numbers is 0 if and only if one or both the numbers are 0. Thus, if we can determine that either a or b is equal to -1, then we know that one of the two factors is 0, and so their product is 0. However, if neither of them equals 0, then their product cannot be 0.
Version I: Answer B – Statement 1 is not sufficient, but statement 2 is.
(1) -10 ≤ a ≤ 20
Partial information. This tells us that -1 is in the range of possible values for a, but a need not equal -1. Not sufficient.
(2) a = -(2 + a)
Full information. Solving this equation for a tells us that its value is -1. This answers the question. Sufficient.
Version II: Answer A – Statement 1 is sufficient, but statement 2 is not.
(1) ab + 1 = -(a + b)
Full information. If we move –(a + b) to the left side of this equation we get ab + a + b + 1 = 0. But this is the same as (a +1)(b + 1) = 0. This answers the question. Sufficient.
(2) b > -10
Partial information. This tells us that -1 is in the range of possible values for b, but b need not equal -1. Not sufficient.
Version III: Answer E – Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
(1) -10 ≤ a ≤ 20
Partial information. This tells us that -1 is in the range of possible values for a, but a need not equal -1. Not sufficient.
(2) b > -10
Partial information. This tells us that -1 is in the range of possible values for b, but b need not equal -1. Not sufficient.
Alone, neither of these statements is sufficient, and together they are not sufficient, because neither of them gives us a specific value for a or b.
Version IV: Answer C – Neither statement 1 nor statement 2 is sufficient, but together they are.
(1) b = a + 2
Partial information. This is one equation in two unknowns, so we cannot determine from it the value of either a or b. Not sufficient.
(2) b + 1 = 2
Partial information. This equation tells us that b = 1, but a could still be -1, so we don’t know the answer. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because we know from statement 2 that b = 1, and substituting this value for b into the equation from statement 2 we can see that a = -1.
Version V: Answer D – Both statement 1 and statement 2 are individually sufficient.
(1) a = -(2 + a)
Full information. Solving this equation for a tells us that its value is -1. This answers the question. Sufficient.
(2) ab + 1 = -(a + b)
Full information. If we move –(a + b) to the left side of this equation we get ab + a + b + 1 = 0. But this is the same as (a +1)(b + 1) = 0. This answers the question. Sufficient.
To practice more problems like this, click here.
Example 3)
Garrett’s charge at grocery store Abra Cadabra included the $50 he spent for food as well as the charge for non-food products. There is no tax for food, but a 6% tax is charged for non-food products. What was the total amount including tax Garrett spent at Abra Cadabra?
Version I.
(1) He spent $8.48 on paper towels, including tax.
(2) His non-food tax, other than for paper towels, was $1.32.
Version II.
(1) He spent $8.48 on paper towels, including tax.
(2) He spent twice as much on soap as he did on paper towels, not including tax.
Version III.
(1) Total tax for the sale was $1.80.
(2) His non-food expenditure, excluding tax, was 60% of his food expenditure.
Version IV.
(1) Total tax for the sale was $1.80.
(2) He spent $8.48 on paper towels, including tax.
Version V.
(1) He spent twice as much on soap as he did on paper towels, not including tax.
(2) Total tax for the sale was $1.80.
Answers: [ Version I: C Version II: E Version III: D Version IV: A Version V: B ]
Explanation:
Version I: Answer C – Neither statement 1 nor statement 2 is sufficient, but together they are.
(1) He spent $8.48 on paper towels, including tax.
Partial information. This might help, but it tells us nothing about other non-food product expenditures. Not sufficient.
(2) His non-food tax, other than for paper towels, was $1.32.
Partial information. This might help, but it tells us nothing about the paper towel expenditure. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because the two statements give us the total tax on non-food, from which we can calculate the total non-food expenditure and the tax. Since we already know the food expenditure, we have the solution to the problem.
Version II: Answer E – Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
(1) He spent $8.48 on paper towels, including tax.
Partial information. This might help, but it tells us nothing about other non-food product expenditures. Not sufficient.
(2) He spent twice as much on soap as he did on paper towels, not including tax.
Partial information. Since this statement says nothing about the amount of paper towel expenditure, it gives us little information. Not sufficient.
Alone, neither of these statements is sufficient, and together they are not sufficient, because even though we can calculate the total expenditure, including tax, on paper towels and soap, we still need to know about other non-food expenditures.
Version III: Answer D – Both statement 1 and statement 2 are individually sufficient.
(1) Total tax for the sale was $1.80.
Full information. Since we know that only non-food products are charged tax, Garrett bought $30 of non-food. Adding tax and the $50 charge for food, we can get the answer to the problem. Sufficient.
(2) His non-food expenditure, excluding tax, was 60% of his food expenditure.
Full information. His food expenditure was $50, so his non-food expenditure was 60% of that, or $30. We know the tax is 6%, so we have all the information we need. Sufficient.
Version IV: Answer A – Statement 1 is sufficient, but statement 2 is not.
(1) Total tax for the sale was $1.80.
Full information. Since we know that only non-food products are charged tax, Garrett bought $30 of non-food. Adding tax and the $50 charge for food, we can get the answer to the problem. Sufficient.
(2) He spent $8.48 on paper towels, including tax.
Partial information. This might help, but it tells us nothing about other non-food product expenditures. Not sufficient.
Version V: Answer B – Statement 1 is not sufficient, but statement 2 is.
(1) He spent twice as much on soap as he did on paper towels, not including tax.
Partial information. Since this statement says nothing about the amount of paper towel expenditure, it gives us little information. Not sufficient.
(2) Total tax for the sale was $1.80.
Full information. Since we know that only non-food products are charged tax, Garrett bought $30 of non-food. Adding tax and the $50 charge for food, we can get the answer to the problem. Sufficient.
To practice more problems like this, click here.
Example 4)
Tricia charges a flat retainer fee of R dollars for up to 40 hours of consulting for a single client in a month. If the client’s work requires over 40 hours, she charges A dollars for each additional hour. The formula, then, for her monthly charge is T = R + EA, where E is the number of hours over 40 that she’s worked. What is the value of R?
(1) 50 hours of work for a client yields over $5000 in fees.
(2) Her fees this month were between $4500 and $5000.
Answer: E – Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
Explanation:
The formula given has 4 unknowns. In the data statements we need to be given either the value of several unknowns, or one or more additional equations, or both.
(1) 50 hours of work for a client yields over $5000 in fees.
Partial information. We need exact numbers, and this only gives us a range – “over $5000.” Not sufficient.
(2) Her fees this month were between $4500 and $5000.
Partial information. We need exact numbers, and this only gives us a range – “between $4500 and $5000.” Not sufficient.
Alone, neither of these statements is sufficient, and together they are not sufficient, because both of them provide only ranges and not specific numbers.
Example 5)
The displacement of an engine is determined from the formula:
\(\begin{align}D = (π/4) b^2s n = .7854 b^2s n\end{align}\)
where b is the engine’s bore, s is its stroke, and n is the number of cylinders in the engine. The bore is the diameter of each cylinder, and the stroke is the distance the piston travels within the engine. What is the displacement of a certain 6 cylinder engine?
(1) Stroke = 2.7 inches, the cylinder radius is 1.75 inches.
(2) The stroke is .8 inches less than the bore.
Answer: A – Statement 1 is sufficient, but statement 2 is not.
Explanation:
This problem is a straightforward plug and grind into a formula. We already have n, the number of cylinders, which is 6, so we just need the bore and the stroke. Remember that the bore is the diameter of the cylinder, while the radius of the cylinder is 1/2 the diameter.
(1) Stroke = 2.7 inches, the cylinder radius is 1.75 inches.
Full information. This gives us the stroke, and the bore is twice the radius, so we have all we need. Sufficient.
(2) The stroke is .8 inches less than the bore.
Partial information. This gives us relative values, and we need specific ones. Not sufficient.
Example 6)
Salvador participated in a CD exchange, to which he took 50 CD’s. In each exchange transaction he either gave up 3 and received 4 (called a “+1” transaction), or gave up 4 and received 3 (called a “-1” transaction). Salvador participated in how many -1 transactions?
(1) Salvador went home with 47 CD’s and participated in at least 6 and no more than 8 transactions.
(2) No CD was involved in more than 1 of Salvador’s transactions, and he got 23 CD’s but gave up 26.
Answer: D – Both statement 1 and statement 2 are individually sufficient.
Explanation:
Let m be the number of -1 transactions, and p the number of +1 transactions. Then m + p is the number of transactions, and m – p = 50 – x, where x is the number of CD’s he took home after the exchange.
(1) Salvador went home with 47 CD’s and participated in at least 6 and no more than 8 transactions.
Full information. We immediately have the equation m – p = 3. Since 3 is odd, then one of m and p is odd, and the other is even, so the number of transactions, m + p is odd. Thus, the second half of the statement tells us that m + p = 7. This gives us two equations in two unknowns, and we easily see that m = 5. Sufficient.
(2) No CD was involved in more than 1 of Salvador’s transactions, and he got 23 CD’s but gave up 26.
Full information. 23 + 26 = 49, so since each transaction involves 7 CD’s, and no CD was in more than one transaction, there must have been 7 transactions, or m + p = 7. Since Salvador had 3 fewer CD’s at the end, then m – p = 3. From these two equations we see that m = 5. Sufficient.
Example 7)
Company J sells 50,000 units of product X per year. Company J decides to lower the price by $.50, in hopes that they will get more sales. How many units do they need to sell so their revenue from product X is the same as before the price change?
(1) The old price of product X is between $2.50 and $3.00.
(2) The new price of product X is $2.00.
Answer: B – Statement 1 is not sufficient, but statement 2 is.
Explanation:
We’re given two values: 50,000 units sold, and a $.50 price cut. Any of several pieces of information could be sufficient to solve the problem: Either the old or the new price, the percent change in price, or the old revenue amount.
(1) The old price of product X is between $2.50 and $3.00.
Partial information. This is an approximate figure, and we need one that’s exact. Not sufficient.
(2) The new price of product X is $2.00.
Full information. From this we compute the old price as $2.50, and the revenue as $125,000. With a new price of $2.00, we need to sell 62,500 units. Sufficient.
Example 8)
If b ≠ -ac and b ≠ -5a, then what’s the value of (5ac + bc)/(ac + b)?
(1) c + d = 3
(2) c – d = 7
Answer: C – Neither statement 1 nor statement 2 is sufficient, but together they are.
Explanation:
This problem, as it stands, looks impossible, but if we can get a favorable value for one or more of the variables, it may look entirely different.
(1) c + d = 3
Partial information. This introduces a new variable, d, and without further information we know nothing new about c. Not sufficient.
(2) c – d = 7
Partial information. This introduces a new variable, d, and without further information we know nothing new about c. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because solving these simultaneously we see that c = 5, and substituting this value for c in the original expression, it reduces to a value of 5.
Example 9)
Heidi drove 300 miles on a recent trip, during which she averaged x miles per hour for the first 100 miles, y miles per hour for the next 120 miles, and z miles per hour for the last 80 miles. What was her average speed for the trip?
(1) x + y + z < 200
(2) She completed the last 80 miles in 1 hour.
Answer: E – Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
Explanation:
The essence of this problem is to use the distance formula, d = rt, to determine average speed. Using this formula we get the average speed as d/t = r, where r is the speed. Since we know the distance is 300 miles, all we need to find is the time it took to travel that distance, and then we can calculate the average speed. Notice that we don’t need to know the speeds, x, y, and z. We just need the total time for the trip.
(1) x + y + z < 200
Partial information. Knowing the sum of the three rates of speed helps us to limit their values, but otherwise gives us nothing. Not sufficient.
(2) She completed the last 80 miles in 1 hour.
Partial information. This gives information about one segment of the trip, and we need the other two. Not sufficient.
Alone, neither of these statements is sufficient, and together they are not sufficient, because statement 2 only gives us the time for completing the last stretch, but statement 1 adds little to that. We now know z = 80, but x + y is still less than 120, and we need exact values for x and y.
Example 10)
Three brothers, Alan, Brian, and Conrad, pick apples in the family orchard. Because of the difference in their ages they pick apples at different rates. The three working together can fill a 10 bushel box in 28 minutes. How long does it take Conrad to fill the box by himself ?
(1) Working together Alan and Brian can fill the box in 42 minutes.
(2) Working by himself, Alan can fill the box in 63 minutes.
Answer: A – Statement 1 is sufficient, but statement 2 is not.
Explanation:
This is a common type of problem which is approached in this case by designating the amount of time it takes one brother, say Brian, to complete the job by defining a variable, b. Thus, in 1 minute Brian can complete 1/b of the job. Alan can complete 1/a of the job in 1 minute, and Conrad 1/c of the job. So, since working together, the 3 brothers complete the entire job in 28 minutes, then they do 1/28 of the job in 1 minute. This translates to 1/a + 1/b + 1/c = 1/28. We’re interested in Conrad’s rate, so we solve as: 1/c = 1/28 – (1/a + 1/b). Thus, if we can find values for both a and b or for (1/a + 1/b), we can find c.
(1) Working together Alan and Brian can fill the box in 42 minutes.
Full information. This says 1/a + 1/b = 1/42, so substituting into the equation we get 1/c = 1/28 – 1/42 = 1/84. So Conrad takes 84 minutes by himself. Sufficient.
(2) Working by himself, Alan can fill the box in 63 minutes.
Partial information. This gives us Alan’s time, but we need Brian’s also. Not sufficient.
Example 11)
Find the value of d.
(1) 4d + 4r = 2(2r + 2d)
(2) 3d + 4r = 2(6 + 2r)
Answer: B – Statement 1 is not sufficient, but statement 2 is.
Explanation:
There is no information given in the statement of the problem, so we have to wait for the help statements, 1 and 2. Thus, solving the problem is a matter of solving equations.
(1) 4d + 4r = 2(2r + 2d)
No information. This is not an equation, but rather an identity that says 4d + 4r = 4d + 4r. Not sufficient.
(2) 3d + 4r = 2(6 + 2r)
Full information. When the right side of this equation is expanded, we get
3d + 4r = 12 + 4r, so
3d = 12, and
d = 4.
Sufficient.
To practice more of these types of problems, click here.