Fractions/Percentages
Every Data Sufficiency (DS) question can have 1 of 5 possible answers, and the possible answers are the same for every DS question. All DS questions are really two questions in one. You’re given a general problem, followed by two supplemental statements. The real problem is to evaluate each of the two statements independently to determine their individual sufficiency to solve the original general problem. As you determine the sufficiency of these statements, you are able to decide which of the following 5 answers to the Data Sufficiency question is the correct answer:
A. Statement 1 is sufficient, but statement 2 is not.
B. Statement 1 is not sufficient, but statement 2 is.
C. Neither statement 1 nor statement 2 is sufficient, but together they are.
D. Both statement 1 and statement 2 are individually sufficient.
E. Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
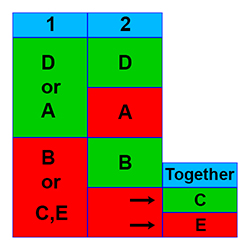
The diagram above gives a pictorial representation of the 5 Data Sufficiency answers. The two statement numbers are shown in blue at the top of the first two columns. Note that green means sufficient, and red means not sufficient. As an example, if both statements 1 and 2 are individually sufficient, then the correct answer is D. For more information on the 5 DS answers, see our videos.
We illustrate these answers for fraction problems with the following 11 examples. Each of the first three examples provides 5 different versions of supplementary statements for the same general problem, and each of these 5 versions yields a different one of the 5 possible answers. The answers to these 5 versions are explained immediately after the problem. After the first 3 examples, we then give 8 additional examples with just one version of the supplementary statements.
[Notice in the first 3 examples that the 5 versions of the supplementary statements provide examples of the 5 different answers, A – E. However, they are not given in A – E order.]
Example 1)
At this year’s Mountain View – Centennial high school football game, were less than 30% of the fans rooting for Centennial?
Version I.
(1) 1 fan in 4 was rooting for Centennial.
(2) The neutral and Mountain View fans outnumbered the Centennial fans by 3 to 1.
Version II.
(1) Over 20% of the fans considered themselves neutral at the game.
(2) Mountain View had twice as many fans as Centennial.
Version III.
(1) Over 20% of the fans considered themselves neutral at the game.
(2) 90% of the neutral fans had attended Centennial High School.
Version IV.
(1) 1 fan in 4 was rooting for Centennial.
(2) Over 20% of the fans considered themselves neutral at the game.
Version V.
(1) 90% of the neutral fans had attended Centennial High School.
(2) 1 fan in 4 was rooting for Centennial.
Answers: [ Version I: D Version II: C Version III: E Version IV: A Version V: B ]
Explanation:
The problem statement gives us no information we can use for calculation.
Version I: Answer D – Both statement 1 and statement 2 are individually sufficient.
(1) 1 fan in 4 was rooting for Centennial.
Full information. This says 25% of the fans were rooting for Centennial, and so it answers the question. Sufficient.
(2) The neutral and Mountain View fans outnumbered the Centennial fans by 3 to 1.
Full information. This says 25% of the fans (1 in 4) were rooting for Centennial, and so it answers the question. Sufficient.
Version II: Answer C – Neither statement 1 nor statement 2 is sufficient, but together they are.
(1) Over 20% of the fans considered themselves neutral at the game.
Partial information. All this tells us is that fewer than 80% of the fans were rooting either for Mountain View or for Centennial. Not sufficient.
(2) Mountain View had twice as many fans as Centennial.
Partial information. We know from this that Centennial had the support of 1/3 of the fans who were not neutral, but unless we know the number of neutral fans we can’t answer the question. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because statement 1 tells us the minimum percentage of neutral fans, and statement 2 says that, of those fans who were not neutral, 1/3 of them rooted for Centennial. But this means that, for example, if Centennial had 30% of the fans, then Mountain View had 60%, for a total of 90%. But no more than 80% of the fans rooted either for Mountain View or Centennial. So Centennial’s share had to be less than 30%.
Version III: Answer E – Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
(1) Over 20% of the fans considered themselves neutral at the game.
Partial information. All this tells us is that fewer than 80% of the fans were rooting either for Mountain View or for Centennial. It says nothing about how the non-neutral fans were divided. Not sufficient.
(2) 90% of the neutral fans had attended Centennial High School.
No information. This statement is irrelevant to the question. (Apparently high school attendance for these fans didn’t translate into commitment.) Not sufficient.
Alone, neither of these statements is sufficient, and together they are not sufficient, because neither statement gives us any information about the number of fans committed to either school.
Version IV: Answer A – Statement 1 is sufficient, but statement 2 is not.
(1) 1 fan in 4 was rooting for Centennial.
Full information. This says 25% of the fans were rooting for Centennial, and so it answers the question. Sufficient.
(2) Over 20% of the fans considered themselves neutral at the game.
Partial information. All this tells us is that fewer than 80% of the fans were rooting either for Mountain View or for Centennial. Not sufficient.
Version V: Answer B – Statement 1 is not sufficient, but statement 2 is.
(1) 90% of the neutral fans had attended Centennial High School.
No information. This statement is irrelevant to the question. (Apparently high school attendance for these fans didn’t translate into commitment.) Not sufficient.
(2) 1 fan in 4 was rooting for Centennial.
Full information. This says 25% of the fans were rooting for Centennial, and so it answers the question. Sufficient.
To practice more of these types of problems, click here.
Example 2)
The ratios of the number of managers to employees in Department X and Department Y are the same. What is the ratio of managers in X to managers in Y?
Version I.
(1) The ratio of managers to employees in Department X is 1 to 10.
(2) Department Y with 100 employees has 150 fewer than Department X.
Version II.
(1) There are 100 employees in Department Y.
(2) Department X has 150 more employees than Y.
Version III.
(1) There are 2.5 times as many employees in Department X as in Department Y.
(2) Department Y with 100 employees has 150 fewer than Department X.
Version IV.
(1) There are 100 employees in Department Y.
(2) The ratio of managers to employees in Department X is 1 to 10.
Version V.
(1) There are 2.5 times as many employees in Department X as in Department Y.
(2) There are 100 employees in Department Y.
Answer: [ Version I: B Version II: C Version III: D Version IV: E Version V: A ]
Explanation:
Version I: Answer B – Statement 1 is not sufficient, but statement 2 is.
(1) The ratio of managers to employees in Department X is 1 to 10.
Partial information. This tells us that the manger/employee ratio in both departments is 1 to 10, but we need the manager/manager ratio across the two departments, and this gives us no information we can use to determine that. Not sufficient.
(2) Department Y with 100 employees has 150 fewer than Department X.
Full information. With 100 employees in Y and 250 in X, there are 2.5 times as many employees in X and therefore 2.5 times as many managers in X as in Y. Sufficient.
Version II: Answer C – Neither statement 1 nor statement 2 is sufficient, but together they are.
(1) There are 100 employees in Department Y.
Partial information. Without knowing the number of employees in X we can’t determine the manager/manager ratio. Not sufficient.
(2) Department X has 150 more employees than Y.
Partial information. Without knowing the number of employees in either department we can’t calculate the manager/manager ratio. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because statement 1 says 100 employees in Y and statement 2 says 250 in X, so there are 2.5 times as many employees in X and therefore 2.5 times as many managers in X as in Y.
Version III: Answer D – Both statement 1 and statement 2 are individually sufficient.
(1) There are 2.5 times as many employees in Department X as in Department Y.
Full information. Since the manager/employee ratio is the same in both departments, if there are 2.5 times as many employees in X as in Y, then there are 2.5 times as many managers in X as in Y. Sufficient.
(2) Department Y with 100 employees has 150 fewer than Department X.
Full information. With 100 employees in Y and 250 in X, there are 2.5 times as many employees in X and therefore 2.5 times as many managers in X as in Y. Sufficient.
Version IV: Answer E – Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
(1) There are 100 employees in Department Y.
Partial information. Without knowing the number of employees in X we can’t determine the manager/manager ratio. Not sufficient.
(2) The ratio of managers to employees in Department X is 1 to 10.
Partial information. This tells us that the manger/employee ratio in both departments is 1 to 10, but we need the manager/manager ratio across the two departments, and this gives us no information we can use to determine that. Not sufficient.
Alone, neither of these statements is sufficient, and together they are not sufficient, because the two only tell us there are 10 managers in Y, but they give us no actual numbers of employees or managers in X.
Version V: Answer A – Statement 1 is sufficient, but statement 2 is not.
(1) There are 2.5 times as many employees in Department X as in Department Y.
Full information. Since the manager/employee ratio is the same in both departments, if there are 2.5 times as many employees in X as in Y, then there are 2.5 times as many managers in X as in Y. Sufficient.
(2) There are 100 employees in Department Y.
Partial information. Without knowing the number of employees in X we can’t determine the manager/manager ratio. Not sufficient.
To practice more of these types of problems, click here.
Example 3)
Barbara has recruited m people as her first level sales force for a multi-level marketing firm. Each of these m people has recruited (m – 1) people to work under them as Barbara’s second level sales force. There is an upper limit of $1000 on the amount of commission she can receive from any one person at either level in her sales force. If last year Barbara received the upper limit from each person on her sales force, as well as $8,000 commissions on her own sales, what is m?
Version I.
(1) Her sales force accounted for 8/9 of her commissions last year.
(2) Including the $8000 on her own sales, she made a total of $72,000 in commissions last year.
Version II.
(1) Including the $8000 on her own sales, she made a total of $72,000 in commissions last year.
(2) Within the upper limit, she receives 5% commission on the sales of each person at either level of her sales force.
Version III.
(1) Within the upper limit, she receives 5% commission on the sales of each person at either level of her sales force.
(2) Each person on her sales force sold at least $20,000 of product last year.
Version IV.
(1) Each person on her sales force sold at least $20,000 of product last year.
(2) Her sales force accounted for 8/9 of her commissions last year.
Version V.
(1) Within the upper limit, she receives 5% commission on the sales of each person at either level of her sales force.
(2) Her sales force made $1,280,000 in sales on which she could receive commissions.
Answer: [ Version I: D Version II: A Version III: E Version IV: B Version V: C ]
Explanation:
Notice that if each of the m people recruited m – 1 people, then there is a total of m(m – 1) people at the second level. Adding in the m first level people, you get \(\begin{align} m(m – 1) + m = m^2 – m + m = m^2\end{align}\) total people in her sales force. So \(\begin{align}m^2\end{align}\) is the number we need to know, and from which we can calculate m.
Version I: Answer D – Both statement 1 and statement 2 are individually sufficient.
(1) Her sales force accounted for 8/9 of her commissions last year.
Full information. Thus, her $8000 commission on her own sales accounts for 1/9 of her commissions, so her commissions from her sales force were 8 times $8000, or $64,000. Since each person contributed $1000 to that amount, there were 64 people, which means m = 8. Sufficient.
(2) Including the $8000 on her own sales, she made a total of $72,000 in commissions last year.
Full information. Subtracting $8000 from $72,000, we get $64,000. Since each person on her sales force contributed $1000, she had 64 people on the force, and m = 8. Sufficient.
Version II: Answer A – Statement 1 is sufficient, but statement 2 is not.
(1) Including the $8000 on her own sales, she made a total of $72,000 in commissions last year.
Full information. Subtracting $8000 from $72,000, we get $64,000. Since each person on her sales force contributed $1000, she had 64 people on the force, and m = 8. Sufficient.
(2) Within the upper limit, she receives 5% commission on the sales of each person at either level of her sales force.
Partial information. This simply tells us that if a sales person sells $20,000 or more, Barbara gets $1000, and if they sell less, say $14,000, she gets $700. This doesn’t help us calculate how many sales people there are in her force. Not sufficient.
Version III: Answer E – Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
(1) Within the upper limit, she receives 5% commission on the sales of each person at either level of her sales force.
Partial information. This simply tells us that if a sales person sells $20,000 or more, Barbara gets $1000, and if they sell less, say $14,000, she gets $700. This doesn’t help us calculate how many sales people there are in her force. Not sufficient.
(2) Each person on her sales force sold at least $20,000 of product last year.
Partial information. Since she received $1000 commission from each person, this just tells us that the commission percentage is 5%. It doesn’t give us any information on m. Not sufficient.
Alone, neither of these statements is sufficient, and together they are not sufficient, because both statements are logically equivalent in the context of the information given in the original statement of the problem.
Version IV: Answer B – Statement 1 is not sufficient, but statement 2 is.
(1) Each person on her sales force sold at least $20,000 of product last year.
Partial information. Since she received $1000 commission from each person, this just tells us that the commission percentage is 5%. It doesn’t give us any information on m. Not sufficient.
(2) Her sales force accounted for 8/9 of her commissions last year.
Full information. Thus, her $8000 commission on her own sales accounts for 1/9 of her commissions, so her commissions from her sales force were 8 times $8000, or $64,000. Since each person contributed $1000 to that amount, there were 64 people, which means m = 8. Sufficient.
Version V: Answer C – Neither statement 1 nor statement 2 is sufficient, but together they are.
(1) Within the upper limit, she receives 5% commission on the sales of each person at either level of her sales force.
Partial information. This simply tells us that if a sales person sells $20,000 or more, Barbara gets $1000, and if they sell less, say $14,000, she gets $700. This doesn’t help us calculate how many sales people there are in her force. Not sufficient.
(2) Her sales force made $1,280,000 in sales on which she could receive commissions.
Partial information. But unless we know the commission percentage rate, we can’t calculate how many people are involved. For example, if the commission rate is 5%, then there are 64 people in her sales force, but if it’s 20%, then there are only 16. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because 5% of $1,280,000 is $64,000, and since each person contributed $1000, there were 64 people, so m = 8
To practice more of these types of problems, click here.
Example 4)
Arcola received offers from Company G and Company H, neither of which was satisfactory. After they each revised their offers, which company offered her the higher starting salary?
(1) H increased their offer by 12% while G’s new offer was 10% above the original.
(2) H increased their offer by $9600, while G’s new offer was $8200 higher.
Answer: C – Neither statement 1 nor statement 2 is sufficient, but together they are.
Explanation:
To determine data sufficiency we just need to know whether we can calculate the amounts of the new offers from the two companies.
(1) H increased their offer by 12% while G’s new offer was 10% above the original.
Partial information. Without knowing the original amount we can’t determine the final. Not sufficient.
(2) H increased their offer by $9600, while G’s new offer was $8200 higher.
Partial information. Without knowing the original amount we can’t determine the final. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because knowing that $9600 is a 12% increase we can compute the original as $80,000 and the final offer from H as $89,600. G’s new offer of $8200 was 10% higher than the original, so the original was $82,000. Therefore, their final offer was $90,200, so G offered the higher starting salary.
Example 5)
For positive integers x and y, is .6 < x/y < .7 ?
(1) y is the smallest prime larger than 37.
(2) x + y > 50.
Answer: E – Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
Explanation:
Once we know x and y, we can convert x/y to the beginning of a decimal fraction. The tenths and hundredths digits tell us the answer to the question.
(1) y is the smallest prime larger than 37.
Partial information. This tells us that y is 41, but without x we can’t answer the question. Not sufficient.
(2) x + y > 50.
Partial information. This tells us essentially nothing of value in determining x/y. Not sufficient.
Alone, neither of these statements is sufficient, and together they are not sufficient, because while the first tells us y is 41, the second only tells us that x is greater than 9, and we need a specific value for x to determine x/y.
Example 6)
An insurance company’s underwriting profit equals their premiums minus deductions for their claims and expenses. Their profit divided by their premiums constitutes their underwriting profit percentage. Company F’s premiums and deductions both increased last year. By what percentage did their underwriting profit change?
(1) This year’s premium of $55 million constituted a 10% increase over last year, and their deductions of $45 million last year increased by 12% this year.
(2) Last year’s premium was $50 million for a 10% underwriting profit, and this year their premium increased to $55 million while their deductions were $50.4 million.
Answer: D – Both statement 1 and statement 2 are individually sufficient.
Explanation:
(1) This year’s premium of $55 million constituted a 10% increase over last year, and their deductions of $45 million last year increased by 12% this year.
Full information. This tells us that last year’s premium was $50 million and deductions were $45 million, so they had $5 million in underwriting profit last year. This year their premium was $55 million and deductions of $50.4 million, so their profit was $4.6 million. From this we can easily calculate percentage change. Sufficient.
(2) Last year’s premium was $50 million for a 10% underwriting profit, and this year their premium increased to $55 million while their deductions were $50.4 million.
Full information. If the underwriting profit was 10% of $50 million, then the deductions were $45 million and the actual profit amount was $5 million. The underwriting profit amount was $4.6 million for this year, and together with last year’s underwriting profit we can calculate the percent change. Sufficient.
Example 7)
Colleen’s rent is 40% of her gross pay. How much does she pay in rent?
(1) Colleen’s take-home pay is $3200.
(2) Her take-home pay is 80% of her gross pay.
Answer: C – Neither statement 1 nor statement 2 is sufficient, but together they are.
Explanation:
If we can compute Colleen’s gross pay, then we can find her rent. We can probably do that through some kind of equation. Or we might find the solution through some other calculation.
(1) Colleen’s take-home pay is $3200.
Partial information. This gives us an actual number, but no percentage relationship to gross pay or to rent. Not sufficient.
(2) Her take-home pay is 80% of her gross pay.
Partial information. This gives us a percentage relationship to gross pay, but no actual number. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because statement 1 tells us her take-home pay, and statement 2 tells us it’s 80% of her gross pay. So her gross pay is $4000, and her rent is $1600.
Example 8)
Each game in bowling consists of 10 frames. For each frame a bowler gets either a strike, a spare, or an open frame. At the Miracle Bowl bowling alley, what was the ratio of strike frames to spare frames last Friday night?
(1) There were 4 times as many spare frames as strike frames.
(2) There were 55 strikes Friday night.
Answer: A – Statement 1 is sufficient, but statement 2 is not.
Explanation:
To determine the ratio asked for we need relationships between spares, strikes, and (possibly) open frames.
(1) There were 4 times as many spare frames as strike frames.
Full information. This tells us the ratio we need is 1 to 4. Sufficient.
(2) There were 55 strikes Friday night.
Partial information. Without the number of spare frames this information doesn’t give us all we need. Not sufficient.
Example 9)
For the past 4 years Salixson Corporation’s product line A has had revenue growth of 8% per year, and product line B has had revenue growth of p% per year. How much was the dollar increase in revenue for product line B last year?
(1) Three years ago product line A’s revenue was $1.2 million.
(2) Three years ago line B’s revenue level was 5/12 of A’s $1.2 million, but its growth has been 2 percentage points higher.
Answer: B – Statement 1 is not sufficient, but statement 2 is.
Explanation:
The statement of the problem gives us little information. Basically, we know there are two product lines of interest, and both of them have a consistent revenue growth for the past 4 years, which for line A is 8%. All the other needed information must come from the other statements. Since we want a dollar value for B’s revenue growth last year, we need a starting point of actual revenue, and the percent by which it’s been growing.
(1) Three years ago product line A’s revenue was $1.2 million.
Partial information. Without a connection to line B, line A’s revenue and growth are irrelevant. Not sufficient.
(2) Three years ago line B’s revenue level was 5/12 of A’s $1.2 million, but its growth has been 2 percentage points higher.
Full information. This gives us an actual revenue figure for line B (5/12 of $1.2 million), and it tells us its percent growth, which is line A’s 8% + 2 percent. Sufficient.
Example 10)
A travel agent charges m% and c% commission for cruises she books in the Mediterranean and the Caribbean, respectively. If she made $88,000 on commissions last year on $2,000,000 in cruise bookings, what is the value of c?
(1) m is 25% higher than c.
(2) The total revenue for the Mediterranean cruises was $400,000 lower than for the Caribbean cruises.
Answer: C – Neither statement 1 nor statement 2 is sufficient, but together they are.
Explanation:
This problem gives us a fair amount of information: total revenue and total commission. But to determine the commission percentages we need to know the breakdown between the Mediterranean and the Caribbean of the total figures we’re given.
(1) m is 25% higher than c.
Partial information. This tells us very little, since m = 5 and c = 4, or m = 8 and c = 6, as well as many other value pairs for m and c satisfy this relationship. Not sufficient.
(2) The total revenue for the Mediterranean cruises was $400,000 lower than for the Caribbean cruises.
Partial information. This gives us the breakdown of revenue from the two locations, but we still need information about the comparative values of m and c. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because the first statement gives us a relationship from which we can derive an equation: m = 5c/4. The second statement tells us the breakdown of the $2,000,000 in revenue: $1,200,000 for the Caribbean and $800,000 for the Mediterranean. We then get a second equation by using the commission received, $88,000: (m/100)∙800,000 + (c/100)∙1,200,000 = 88,000. This gives us two equations in the two unknowns, m and c, and we can solve for both m and c.
Example 11)
Three sisters, Abby, Hope, and Maria, have heights in varying proportional relationships. If a, h, and m are their respective heights in inches, then a/h, h/m, m/a are some of the various ratios of their heights. Who is the shortest?
(1) a/m < 1
(2) h/m < 1
Answer: E – Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
Explanation:
Using the indicated variables and making comparisons, the following are true: If a/h < 1, then h/a > 1, and Abby is shorter than Hope. Also, if a/h < m/h, then Abby is shorter than Maria. These facts help us to understand the various comparisons that are shown in the statements (1) and (2).
(1) a/m < 1
Partial information. This says Abby is shorter than Maria, but says nothing about her height in comparison to Hope. Not sufficient.
(2) h/m < 1
Partial information. This says Hope is shorter than Maria, but says nothing about her height in comparison to Abby. Not sufficient.
Alone, neither of these statements is sufficient, and together they are not sufficient, because though Abby and Hope are both shorter than Maria, we know nothing about their heights in comparison to each other.
To practice more of these types of problems, click here.