Geometry
We deal here with two types of geometry problems: Those from coordinate geometry and those from plane geometry. Coordinate geometry problems are geometry problems in the xy-coordinate plane. They often are concerned with specific coordinate values for points, and they include concepts such as slope of lines and x and y intercepts. Plane geometry problems are typically expressed without regard to the xy-coordinate plane, and are the more traditional geometry problems dealing with triangles and circles.
On this page we provide examples of both types of geometry problems, as follows:
- 4 Coordinate Geometry problems
- 2 Circles problems
- 1 Triangles problem
- 1 Volume problem
To practice more of these types of problems, click here.
Coordinate Geometry Example 1, Part 1)
What is the y-intercept of the line defined by mx + 4y = 9?
A. 9/4
B. 9
C. 9/m
D. m
E. 4/m
Explanation: The y-intercept of a line whose equation is known can be found by putting the equation in the slope-intercept form, y = mx + b, where m is the slope of the line, and b is its y-intercept. This is true, because the y-intercept is the place where the line crosses the y-axis, and at that point the value for the x-coordinate of the intercept is 0. If x is 0 in this equation, then y = b. So to find the y-intercept of this line, we put the equation in the slope intercept form:
mx + 4y = 9
4y = 9 – mx
y = 9/4 – mx/4
So the y-intercept is 9/4, and A is the correct answer.
An easier solution in this case would be to simply set x = 0 in the original equation, and we would get
4y = 9
y = 9/4
Since the y-intercept is the value of y when x = 0, then this is all we have to do.
Coordinate Geometry Example 1, Part 2)
What is the x-intercept of the line defined by mx + 4y = 9?
A. 9/4
B. 9
C. 9/m
D. m
E. 4/m
Explanation: The x-intercept occurs when y is 0. So we simply set y = 0 in the equation and solve for x.
mx = 9
x = 9/m
So answer C is correct.
Coordinate Geometry Example 1, Part 3)
On the line defined by mx + 4y = 9, what is the value of m when x = 0?
A. 9/4y
B. 9/4
C. 9/x
D. 9 – 4y
E. Indeterminate
Explanation: This is somewhat of a trick question, because if x = 0 we can find the value for y, but not the value for m. Any value for m will work in the equation if x is 0. So, m is indeterminate – that is, it cannot be determined.
So answer E is correct.
Coordinate Geometry Example 2)
A circle centered at (-3, 4) passes through the origin. What is its radius?
A. 3
B. 4
C. 5
D. 7
E. 6 π
Explanation: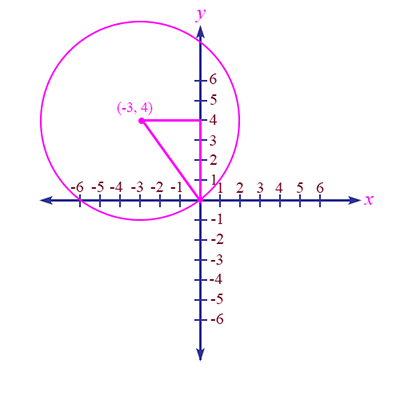 
If the circle shown in the diagram passes through the origin, then its radius r is the distance from the point (-3, 4) to the origin (0,0). This distance can be calculated by the Pythagorean theorem, because the radius from the center of the circle to the origin is the hypotenuse of the right triangle that has as one leg, the line from the center to the y-axis, and whose length is 3, and as the other leg, the portion of the y-axis that goes from 4 down to 0, and whose length is 4. Thus, we have the equation:
\(\begin{align}3^2 + 4^2 = r^2\end{align}\)
\(\begin{align}9 + 16 = r^2\end{align}\)
\(\begin{align}25 = r^2\end{align}\)
\(\begin{align}5 = r\end{align}\)
So answer C is correct.
To practice more problems like these, click here.
Circles Example 1, Part 1)
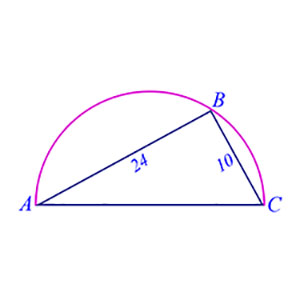The diagram above shows a triangle embedded in a semicircle. If the length of segment AB is 24, and of segment BC is 10, what is the area of the semicircle?
A. \(\begin{align}(12)^2 \cdot\, \frac{π}{3}\end{align}\)
B. \(\begin{align}(6)^2 \cdot\, \frac{π}{2}\end{align}\)
C. \(\begin{align}(24)^2 \cdot\, \frac{π}{10}\end{align}\)
D. \(\begin{align}(13)^2 \cdot\, \frac{π}{2}\end{align}\)
E. \(\begin{align}(10)^2 \cdot\, \frac{π}{2}\end{align}\)
Explanation: The area of a semicircle is half the area of a circle, and so is\(\begin{align}\frac{πr^2}{2}\end{align}\), where r is the radius of the circle.
Important fact! A triangle embedded in a semicircle is a right triangle. Therefore, the hypotenuse of the triangle is the diameter d of the semicircle, and so we can calculate the radius by using the Pythagorean theorem:
\(\begin{align}d^2 = 24^2 + 10^2\end{align}\)
\(\begin{align}d^2 = 576 + 100 = 676\end{align}\)
\(\begin{align}d = 26\end{align}\)
\(\begin{align}r = 13\end{align}\)
Thus, the area of the semicircle is\(\begin{align}(13)^2 \cdot\, \frac{π}{2}\end{align}\)
So D is the correct answer.
Circles Example 1, Part 2)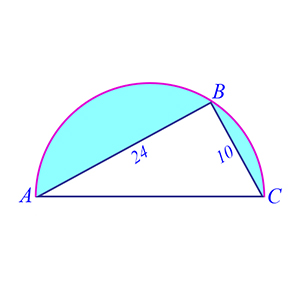 
Again, we have a triangle embedded in a semicircle. In the triangle shown above, if the length of segment AB is 24, and of segment BC is 10, what is the area of the semicircle outside the triangle?
A.\(\begin{align}(6)^2 \cdot\, \frac{π}{2}-\, 120\end{align}\)
B.\(\begin{align}(36)^2\cdot\, \frac{π}{2}-\, 144\end{align}\)
C.\(\begin{align}(24)^2\cdot\, \frac{π}{2}-\, 156\end{align}\)
D.\(\begin{align}(13)^2\cdot\, \frac{π}{2}-\, 120\end{align}\)
E.\(\begin{align}(12)^2\cdot\, \frac{π}{2}-\, 144\end{align}\)
Explanation: The area of a semicircle is half the area of a circle, and so is\(\begin{align}\frac{πr^2}{2}\end{align}\). Important fact! A triangle embedded in a semicircle is a right triangle. Therefore, the diameter d of this semicircle is the hypotenuse of the triangle, and so:
\(\begin{align}d^2 = 24^2 + 10^2\end{align}\)
\(\begin{align}d^2 = 576 + 100 = 676\end{align}\)
\(\begin{align}d = 26\end{align}\)
\(\begin{align}r = 13\end{align}\)
So, the area of the semicircle is \(\begin{align}(13)^2 \cdot\, \frac{π}{2}\end{align}\). The area of the triangle is 1/2 the base times the height, and since the base is 10 and the height is 24, then the area of the triangle is 120. Thus, the area of the semicircle outside the triangle – the shaded area in the diagram – is
\(\begin{align}(13)^2\cdot\, \frac{π}{2}-\, 120\end{align}\)
So D is the correct answer.
To practice more problems like this, click here.
Triangles Example 1)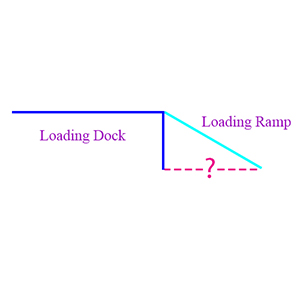 
A loading ramp for a warehouse is 10 feet long, and makes a\(\begin{align}30^\circ\end{align}\)angle with the ground. How many feet from the warehouse wall is the bottom of the ramp?
A. \(\begin{align}10\sqrt{30}\end{align}\)
B. \(\begin{align}8\sqrt{3}\end{align}\)
C. \(\begin{align}\frac{5}{\sqrt{10}}\end{align}\)
D. \(\begin{align}\frac{8}{\sqrt{5}}\end{align}\)
E. \(\begin{align}5\sqrt{3}\end{align}\)
Explanation: This is a typical\(\begin{align}30, 60, 90\end{align}\)triangle problem. That is, since the angle of the warehouse wall with the ground is\(\begin{align}90^\circ,\end{align}\)and since the angle of the ramp with the ground is\(\begin{align}30^\circ,\end{align}\)then the other angle in the triangle is\(\begin{align}60^\circ.\end{align}\)Therefore, the lengths of the sides of the triangle with these angles are in the ratio\(\begin{align}1\colon2\colon\sqrt{3},\end{align}\)where\(\begin{align}2\end{align}\)is the hypotenuse, and\(\begin{align}\sqrt{3}\end{align}\)is the length of the leg from the warehouse wall to the bottom of the ramp. Since the length of the ramp is 10 feet, then the distance of the bottom of the ramp to the warehouse wall is\(\begin{align}5\sqrt{3}.\end{align}\)
So E is the correct answer.
For more problems like this, click here.
Volume Example 1)
A container company produces storage cylinders that store x gallons. If they were to make the cylinder more tube-shaped by reducing the diameter to 1/3 its current size, but doubling its height, how much would the new cylinder store, in terms of x?
A. 2/3 x
B. 2/9 x
C. 1/6 x
D. 2/5 x
E. 1/4 x
Explanation: The volume of a cylinder is\(\begin{align}πr^2h,\end{align}\)where r is the radius of the cylinder, and h is its height. If the diameter is 1/3 its previous size, then so will its radius be 1/3 its size, and the radius squared will be 1/9 of the previous radius squared. So with no other change than to the radius, the new volume will be
1/9 x
But the height is doubled, so the new volume is
2/9 x
Therefore, B is the correct answer.
For more problems like this, click here.