Basics of Inequalities

Click here for definitions of terms

An inequality is a mathematical statement that two quantities are comparable but not necessarily equal. Usually, it includes an indication as to which quantity is greater or less. For example: x ≤ 3, says x can be 3, but it might be less than 3. Alternately, x < 3 says x is definitely less than 3. Inequalities are expressed using the following operators: <, >, ≤, ≥, ≠.

Inequalities are solved just as equations are, with one notable exception. In an inequality, if you multiply or divide both sides by the same negative number, then you reverse the direction of the inequality. For example,

3 – 5x < 30
-5x < 27
5x > -27
x > -27/5

Notice that as we went from the second to the third steps we multiplied both sides of the inequality by -1. This reversed the order of the inequality. The rest of the inequality was solved as if it were an equation.

Often, inequalities are used with absolute values to define ranges of values.

The absolute value of a number is the distance the number is from 0. If x is a positive real number, then its absolute value, |x|, is x. For example, if x is 3, then |x| = |3| = 3. If x is a negative real number, then |x| = -x. For example, if x is -3, then |x| = |-3| = -(-3) = 3. Notice that both 3 and -3 are the same distance, 3, from 0.

Suppose now that we have the statement

|x| ≥ 5

What does this translate into – that is, for what values of x is it true? Obviously, if x is greater than or equal to 5, then the statement is true. Are there other values for x that would make the statement true? The answer is yes. If x is less than or equal to -5, then the statement is true. These are all the values for which |x| ≥ 5 is true: Either x is ≥ 5 or x ≤ -5. The line below shows these values graphically. The blue portions indicate the values on the real line where the statement is true, whereas the red portion indicates the values for which the statement is false. Notice that the true portion includes the number -5 and 5.

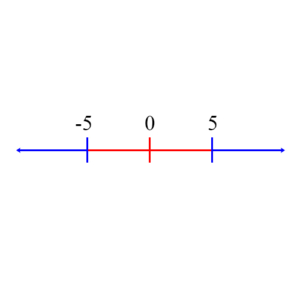These values can be determined more systematically. We start with the original statement:

|x| ≥ 5

and we note that this will be true when x > 0 if x ≥ 5. This is obvious. But what if x < 0? Then we use the definition of absolute value which says that if x < 0, then |x| = -x. So when will -x be greater than or equal to 5?

-x ≥ 5
-1(-x) ≤ -1(5)
x ≤ -5

Notice that in the second line of this derivation we changed the direction of the inequality because we multiplied both sides by a negative number (-1). The final answer, of course, is the same answer we determined above, but in this case we calculated it through the solution of the inequality.

Let’s try a more complex example.

|3x + 1| ≥ 5

If 3x + 1 is positive, then its absolute value is simply 3x + 1. For what values of x, then, will the statement be true?

3x + 1 ≥ 5
3x ≥ 4
x ≥ 4/3

But what if 3x + 1 is negative? In this case, its absolute value is -(3x +1) = -3x – 1. For what values of x will the statement be true now?

-3x – 1 ≥ 5
-3x ≥ 6
x ≤ -2

These results can be summed up by saying the statement will be true whenever

x ≤ -2 or x ≥ 4/3

as shown in the figure below.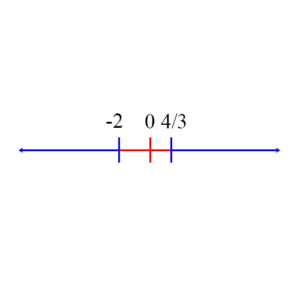Sample Inequality and Absolute Value Problems