Integers – Definitions of Terms

Consecutive Even Integers: A sequence of even integers, each element of which is 2 greater than the previous element. Examples:

8, 10, 12, 14, 16, …

-4, -2, 0, 2, 4, 6, …

Consecutive Integers: A sequence of integers, each element of which is 1 greater than the previous element. Examples:

0, 1, 2, 3, 4, …

-3, -2, -1, 0, 1, 2, …

Consecutive Odd Integers: A sequence of odd integers, each element of which is 2 greater than the previous element. Examples:

7, 9, 11, 13, 15, …

-5, -3, -1, 1, 3, …

Divisible: This states a relationship between two integers. a is divisible by b, if for some integer n, a = bn.

Divisor: This states a relationship between two integers. b is a divisor of a, if for some integer n, a = bn.

Even Integer: An integer divisible by 2. Examples: 0, 2, 4, 6, 8

Factor: A component of a multiplication product. For example, 2 and 3 are factors of 6, since 6 = 2 x 3. Also, the factors of \(\begin{align}x^2 + 5x + 6\end{align}\) are (x + 2) and (x + 3), since (x + 2)(x + 3) = \(\begin{align}x^2 + 5x + 6\end{align}\).

Factorial: The operation of multiplying a positive integer by every positive integer less than or equal to it. For example, 4 factorial (written 4!) is

\(\begin{align} 4 \times 3 \times 2 \times 1 = 24\end{align}\)

Greatest Common Factor (Divisor): The largest number which evenly divides two or more numbers. The greatest common factor (or the greatest common divisor) of 20 and 24, for example, is 4. Even though 2 evenly divides both numbers, it’s smaller than 4, so 4 is the greatest common factor.

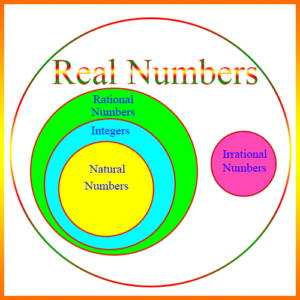
Integer: A whole number, which can be positive, negative, or zero. For example, 5, 17, -8, -365, and 0 are integers. The figure shows the Integers as a subset of the Rational Numbers.

Least Common Multiple (lcm): The smallest number which is a multiple of two or more numbers. For example, the least common multiple of 6 and 10 is 30, since even though 60 is a multiple of both numbers, 30 is also and is smaller than 60.

Multiple: An integer a is a multiple of b if there is some integer n, such that a = bn.

Natural Number: A positive integer, or “counting number.” 1, 2, 3, etc. are natural numbers. 0 is sometimes considered a natural number also.

Odd Integer: An integer which is not evenly divisible by 2. Examples: 1, 3, 5, 7.

Prime Factorization: The representation of a positive integer as a product of powers of primes (a p-p-p!). For example, the prime factorization of 180 is

\(\begin{align} 2^2 \times 3^2 \times 5\end{align}\)

since the only prime numbers that divide 180 are 2 (twice), 3 (twice), and 5.

Prime Number: An integer greater than 1 which can only be evenly divided by itself or by 1. Examples: 2, 3, 5, 17, 43.

Quotient: The result of a division operation. It’s possible the operation may yield a remainder as well as a quotient. Thus, if we divide 20 by 3, then the quotient is 6, but there is a remainder of 2.

Remainder: If an integer n is not evenly divisible by another integer k, then we can find integers q and r, such that n = qk + r, q is maximized, and r < k. The integer q is called the quotient, and r is the remainder. Example: Let n be 25 and k be 7. Then q is 3 and r is 4, because 25 = 3·7 + 4.