Real Numbers – Definitions of Terms

Absolute Value: The distance a number is from 0. If x is a positive real number, then its absolute value, |x|, is x. For example, if x is 3, then |x| = |3| = 3. If x is a negative real number, then |x| = -x. For example, if x is -3, then |x| = |-3| = -(-3) = 3. Notice that both 3 and -3 are the same distance, 3, from 0.

Decimal Number: A number defined using the decimal or base ten system. Its decimal point separates the integer part from the fractional part, with each numeral to the right of the decimal representing some negative power of 10, and each numeral to the left representing some non-negative power of 10. Example:

8,765.4321

In this example, 8 is in the 1000’s (or 10³) position, 7 in the 100’s (10²) position, etc.

We say that 5 is in the “units” position, and 4 is in the tenths or 10^-1 position.

Decimal Point: The dot or period in a decimal number which separates the integer part on the left from the fractional part on the right.

Integer: A whole number, which can be positive, negative, or zero. For example, 5, 17, -8, -365, and 0 are integers.

Irrational Number: A number which is a real number, but is not a rational number. That is, it cannot be expressed as a ratio of two integers. \(\begin{align} \sqrt{2}\end{align}\) and \(\begin{align}\pi\end{align}\) are irrational numbers.

Natural Number: A positive integer, or “counting number.” 1, 2, 3, etc. are natural numbers. 0 is sometimes considered a natural number also.

Rational Number: A number which is a fraction or “ratio” between two integers. 2/5, 25/8, -4/3, and 0 are all rational numbers. Every integer is a rational number. Rational numbers are also considered real numbers.

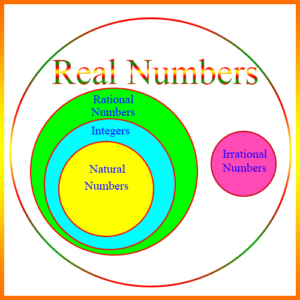
Real Number: A number which is either a rational or an irrational number. The figure shows the relationship between the real numbers and its major subsets.

Repeating Decimal: A decimal number which repeats a pattern of integers infinitely. It is always equivalent to some rational number. Example: The infinitely repeating decimal .428571428571428571… is actually the rational number 3/7.

Root of a Number: A real number which when raised to the appropriate power yields the original number. Examples: The square root of 2, when multiplied by itself equals 2. The cubed root of 5, when raised to the 3rd power equals 5.

Scientific Notation: A representation of a decimal or integer as a value between 1 and 10, multiplied by a power of 10. Examples:

\(\begin{align}99999 = 9.9999 \times 10^4\end{align}\)

\(\begin{align}.099 = 9.9 \times 10^{-2}\end{align}\)

The exponent for 10 indicates the number of places the decimal point should be moved to the right or to the left. In the first example above, the exponent is 4, so to get the original number, you move the decimal point 4 places to the right. In the second example, the exponent is -2, so you move the decimal point 2 places to the left.

Square Root: A number which when multiplied by itself yields the number for which it is the square root. Example: 3 is the square root of 9, because 3 × 3 = 9. The square roots of most numbers are not rational numbers. For example, the square roots of 2, 3, 5, 7, etc. are real numbers, but they are not rational numbers.