Statistical Functions
Every Data Sufficiency (DS) question can have 1 of 5 possible answers, and the possible answers are the same for every DS question. All DS questions are really two questions in one. You’re given a general problem, followed by two supplemental statements. The real problem is to evaluate each of the two statements independently to determine their individual sufficiency to solve the original general problem. As you determine the sufficiency of these statements, you are able to decide which of the following 5 answers to the Data Sufficiency question is the correct answer:
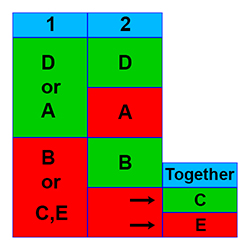
A. Statement 1 is sufficient, but statement 2 is not.
B. Statement 1 is not sufficient, but statement 2 is.
C. Neither statement 1 nor statement 2 is sufficient, but together they are.
D. Both statement 1 and statement 2 are individually sufficient.
E. Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
The diagram above gives a pictorial representation of the 5 Data Sufficiency answers. The two statement numbers are shown in blue at the top of the first two columns. Note that green means sufficient, and red means not sufficient. As an example, if both statements 1 and 2 are individually sufficient, then the correct answer is D. For more information on the 5 DS answers, see our videos.
We illustrate these answers for statistical function problems with the following 3 examples. Each of the first two examples provides 5 different versions of supplementary statements for the same general problem, and each of these 5 versions yields a different one of the 5 possible answers. The answers to these 5 versions are explained immediately after the problem. After the first 2 examples, we then give one additional example with just one version of the supplementary statements.
[Notice in the first 2 examples that the 5 versions of the supplementary statements provide examples of the 5 different answers, A – E. However, they are not given in A – E order.]
Example 1)
The number of laptop and tablet computers in each of 10 homes was determined in a survey. What was the standard deviation of the number of computers?
Version I.
(1) The variance was between 2 and 3.
(2) 4 of the homes had the same number of computers, 3 homes had 7, 3 homes had 3, and the mean was 5.
Version II.
(1) The mean was 5.
(2) 4 of the homes had the same number of computers, 3 homes had 7, 3 homes had 3.
Version III.
(1) 4 of the homes had the same number of computers, 3 homes had 7, 3 homes had 3, and the mean was 5.
(2) The variance was 2.4
Version IV.
(1) The variance was between 2 and 3.
(2) The mean was 5.
Version V.
(1) 4 of the homes had the same number of computers, 3 homes had 7, 3 homes had 3, and the mean was 5.
(2) The variance was between 2 and 3.
Answers: [ Version I: B Version II: C Version III: D Version IV: E Version V: A ]
Explanation:
If we have all the data from the survey we can easily calculate the mean, variance, and standard deviation. Thus, look for whether the statements give us the basic survey data.
Version I: Answer B – Statement 1 is not sufficient, but statement 2 is.
(1) The variance was between 2 and 3.
Partial information. For this we need an exact value, not a range of values. Not sufficient.
(2) 4 of the homes had the same number of computers, 3 homes had 7, 3 homes had 3, and the mean was 5.
Full information. The six homes whose numbers we have been given have a mean of 5. Since there were only 10 homes, then the 4 homes having the same number must have also had 5, because the overall mean is 5. From this we can calculate the standard deviation. Sufficient.
Version II: Answer C – Neither statement 1 nor statement 2 is sufficient, but together they are.
(1) The mean was 5.
Partial information. We need specific numbers for individual homes. Not sufficient.
(2) 4 of the homes had the same number of computers, 3 homes had 7, and 3 homes had 3.
Partial information. Now we just need to know the number of computers in the 4 homes that had the same number. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because the six homes whose numbers we have been given have a mean of 5. Since there were only 10 homes, then the 4 homes having the same number must have also had 5 computers, because the overall mean is 5. From this we can calculate the standard deviation.
Version III: Answer D – Both statement 1 and statement 2 are individually sufficient.
(1) 4 of the homes had the same number of computers, 3 homes had 7, 3 homes had 3, and the mean was 5.
Full information. The six homes whose numbers we have been given have a mean of 5. Since there were only 10 homes, then the 4 homes having the same number must have also had 5, because the overall mean is 5. From this we can calculate the standard deviation. Sufficient.
(2) The variance was 2.4.
Full information. The standard deviation is the square root of the variance. Sufficient.
Version IV: Answer E – Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
(1) The variance was between 2 and 3.
Partial information. For this we need an exact value, not a range of values. Not sufficient.
(2) The mean was 5.
Partial information. Now we need the numbers of computers in individual homes. Not sufficient.
Alone, neither of these statements is sufficient, and together they are not sufficient, because neither tells us anything exact about the numbers of computers in individual homes.
Version V: Answer A – Statement 1 is sufficient, but statement 2 is not.
(1) 4 of the homes had the same number of computers, 3 homes had 7, 3 homes had 3, and the mean was 5.
Full information. The six homes whose numbers we have been given have a mean of 5. Since there were only 10 homes, then the 4 homes having the same number must have also had 5, because the overall mean is 5. From this we can calculate the standard deviation. Sufficient.
(2) The variance was between 2 and 3.
Partial information. For this we need an exact value, not a range of values. Not sufficient.
To practice more of these types of problems, click here.
Example 2)
What is the median of the starting salaries paid by Company D last year?
Version I.
(1) At $50,000 the highest paid of the 3 new people received $5,000 more than the lowest and $2,000 more than the second lowest.
(2) The difference between the lowest and second lowest starting salaries was $3,000.
Version II.
(1) At $50,000 the highest paid of the 3 new people received $5,000 more than the lowest and $2,000 more than the second lowest.
(2) The $50,000 salary of the highest paid new employee was 1/24 above the median salary paid to new employees.
Version III.
(1) The highest paid received $5,000 more than the lowest and $2,000 more than the second lowest.
(2) The difference between the lowest and median starting salaries was $3,000.
Version IV.
(1) The highest paid received $5,000 more than the lowest and $2,000 more than the second lowest.
(2) At $50,000 the highest paid of the 3 new people received $5,000 more than the lowest and $2,000 more than the second lowest.
Version V.
(1) At $50,000 the highest paid received $5,000 more than the lowest, and $2,000 more than the second lowest.
(2) The difference between the lowest and median starting salaries was $3,000.
Answers: [ Version I: A Version II: D Version III: E Version IV: B Version V: C ]
Explanation:
Since we’re looking for the median it would help us to know how many new employees were hired, and what relationships existed between their starting salaries. Also, we need a specific salary as an anchor to help us calculate the actual median.
Version I: Answer A – Statement 1 is sufficient, but statement 2 is not.
(1) At $50,000 the highest paid of the 3 new people received $5,000 more than the lowest and $2,000 more than the second lowest.
Full information. Since there were only 3 new employees, the median salary is that paid to the second lowest, which is $50,000 – $2,000. Sufficient.
(2) The difference between the lowest and second lowest starting salaries was $3,000.
Partial information. This tells us nothing about the number of new employees, nor an actual salary to which we can tie the information in the statement. Not sufficient.
Version II: Answer D – Both statement 1 and statement 2 are individually sufficient.
(1) At $50,000 the highest paid of the 3 new people received $5,000 more than the lowest and $2,000 more than the second lowest.
Full information. Since there were only 3 new employees, the median salary is that paid to the second lowest, which is $50,000 – $2,000. Sufficient.
(2) The $50,000 salary of the highest paid new employee was 1/24 above the median salary paid to new employees.
Full information. This gives us a simple equation: 25/24 x median = 50,000, from which we can determine that the median is $48,000. Sufficient.
Version III: Answer E – Neither statement 1 nor statement 2 is sufficient, and together they are not sufficient.
(1) The highest paid received $5,000 more than the lowest and $2,000 more than the second lowest.
Partial information. This tells us nothing about the median since we have no idea how many salaries there are, nor a specific value for any salary. Not sufficient.
(2) The difference between the lowest and median starting salaries was $3,000.
Partial information. If we had a specific value for the lowest salary, we could calculate the median, but we don’t have a specific value. Not sufficient.
Alone, neither of these statements is sufficient, and together they are not sufficient, because there is no specific value given in either statement for any new employee’s salary.
Version IV: Answer B – Statement 1 is not sufficient, but statement 2 is.
(1) The highest paid received $5,000 more than the lowest and $2,000 more than the second lowest.
Partial information. This tells us nothing about the median since we have no idea how many salaries there are, nor a specific value for any salary. Not sufficient.
(2) At $50,000 the highest paid of the 3 new people received $5,000 more than the lowest and $2,000 more than the second lowest.
Full information. Since there were only 3 new employees, the median salary is that paid to the second lowest, which is $50,000 – $2,000. Sufficient.
Version V: Answer C – Neither statement 1 nor statement 2 is sufficient, but together they are.
(1) At $50,000 the highest paid received $5,000 more than the lowest and $2,000 more than the second lowest.
Partial information. This statement doesn’t give us any information about the number of new employees, so we can’t calculate the median. Not sufficient.
(2) The difference between the lowest and median starting salaries was $3,000.
Partial information. This is only relative information, from which it’s impossible to calculate the actual median. Not sufficient.
Alone, neither of these statements is sufficient, but together they are sufficient, because statement 1 tells us the highest paid is $50,000, which is $5,000 more than the lowest, and statement 2 tells us the difference between the lowest and the median is $3,000. From this we conclude that the median is $2,000 less than $50,000 or $48,000.
To practice more of these types of problems, click here.
Example 3)
A department store has 70 shirts for sale of types Brand A and Brand B, and their average price is $22.00. Is the average price of Brand B shirts $25 or more?
(1) There were at least 12 more Brand A shirts than Brand B shirts.
(2) There were over 40 Brand A shirts, and their average price was under $18.
Answer: B – Statement 1 is not sufficient, but statement 2 is.
Explanation:
Both Brand A and Brand B shirts contribute to the average price of all shirts. If there are few Brand A shirts, then the Brand B shirts would influence the average price significantly, and so their average is likely to be close to $22. However, if there were a very large number of Brand A shirts, then the average price of all the shirts would be heavily weighted toward the average of the Brand A shirts. Thus, information about Brand A prices could be sufficient to decide the question.
Note also that the total price of all 70 shirts is $1540. This number will be needed in calculations.
(1) There were at least 12 more Brand A shirts than Brand B shirts.
Partial information. This gives us ranges of number of shirts of each brand, but no cost information which is essential in the computation of average cost. Not sufficient.
(2) There were over 40 Brand A shirts, and their average price was under $18.
Full information. There must be at least 41 Brand A shirts, and if they all cost exactly $18, then they would account for at least $738 of the $1540. This would leave no more than 29 Brand B shirts whose total cost is $802. This is an average of more than $27. If there are more than 41 Brand A shirts or if their average price was somewhat less than $18, then the average price for Brand B shirts must be even higher. Sufficient.
To practice more of these types of problems, click here.