Basics of Word Problems

Word problems can take many forms, but certain types tend to appear repeatedly, and they can be approached in a very definite manner. Knowing their characteristics makes it easier to move directly to a solution. On this page we discuss ten standard word problem types.

Sample Word Problems

 

Interpreting Graphically Displayed Data

Pie charts, bar graphs, and line graphs are examples of data being presented in ways that make it more accessible for understanding. Being able to read and interpret such charts is an essential skill in most organizational settings.

Example 1: 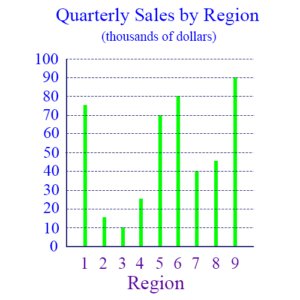In the figure above, how many regions had quarterly sales above $50,000 but less than $60,000?

Solution: The top of each green bar indicates the level of sales for the region whose number is at the bottom of the bar. Thus, region 1 had about $75,000 in sales, region 2 had about $15,000 in sales, etc. If you look at the $50,000 and the $60,000 levels, you can see that no bar actually has its maximum between these two levels. So the answer to the question is 0.

Example 2:

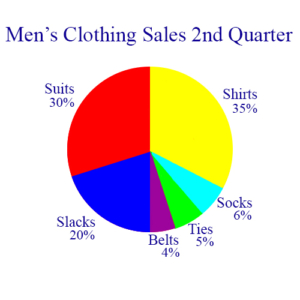
The pie chart above shows the distribution by percent of the revenue from sales of various types of men’s clothes during a 3 month period. If the total sales during this time was $50,000, then how much of that came from suits and shirts?

Solution: Suits constituted 30% and shirts 35% of the revenue for that quarter, or, in other words, they accounted for 65% of the revenue. If the total revenue was $50,000, then suits and shirts were

65% of $50,000 = .65 × 50,000 = $32,500


Example 3: Using the pie chart again, how much more revenue came from the sale of slacks than from the sale of belts, ties, and socks?

Solution: Slacks accounted for 20%, and belts, ties, and socks together accounted for 15%, a difference of 5%. Applying this percentage to the $50,000 of total revenue

.05 × 50,000 = $2,500

 

Discount/Markup Problems

Formulas:

Discounts:

\(\begin{align} DiscountedPrice = (1 – \frac{DiscountPercent}{100}) \times OldPrice \end{align}\)

\(\begin{align}DiscountPercent = \frac{OldPrice – NewPrice}{OldPrice} \times 100 \end{align}\)

Markups:

\(\begin{align}MarkupPrice = Cost + \frac{MarkupPercent}{100} \times Cost \end{align}\)

\(\begin{align}MarkupPercent = \frac{Price – Cost}{Cost} \times 100 \end{align}\)

Discount problems are normally percentage problems. Suppose we have a retail store, and in order to sell an item we decide to discount its price by x percent, then what is the new price? This is shown in the first formula above.

Or we may have to look at the problem in reverse: We know both the old and the new prices, so what is the discount percent? This is shown in the second formula.

Markups use the same concept, but going the other direction: Suppose we need to determine the selling price of items in a newly received shipment. Then if our normal practice is to mark the price up 25% above the cost, what will the selling price be? This is shown in the third formula.

Or, looking at it the other way, if we know both the selling price and the original cost, then what is the markup percentage? And this is the fourth formula.

This same concept also applies to determining the percentage salary increase when we compare an old and a new salary. Our company’s practice may be to give employees annual increases of 5-15%, depending on the quality of their annual review. If we give Mary Ann a 12% increase, then what is her new salary? Or, looking at it the other way, if Sam is offered $10,000 more to go to work for another company, what is the percent salary increase the new company is offering above his current salary?

The four formulas above show how we can calculate percents and values, both for discounts and markups, given the information required by the formulas.

Example 1: Electrons Unlimited has discounted some laptop computers from $300 to $180. What is the percent of this discount?

Solution: Using the second formula above, we subtract the new price from the old price to get the amount discounted:

300 – 180 = 120

We then divide by the old price and multiply by 100 to get the percent:

120/300 × 100 = 120/3 = 40%


Example 2: When Electrons Unlimited obtained 30 of a certain brand of television, they marked the price up 20% from their cost. If their cost was $500, then what was the marked up selling price?

Solution: Using the third formula above we simply multiply the cost by 20% = .2 and add the result to the cost to obtain the marked up selling price:

.2 × 500 + 500 = 100 + 500 = 600

 

Geometry Problems

Word problems involving geometry concepts often are concerned with areas, volumes, and perimeters. Applying the basics of geometry thus becomes a helpful skill for solving these problems.

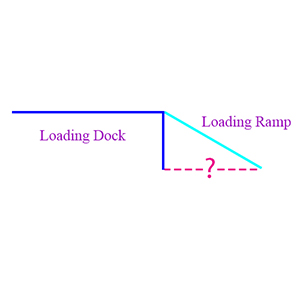
Example 1: Below is a simple diagram showing a loading dock and the ramp leading up to it. If we assume the loading dock makes a right angle with the ground, the ramp makes a 30° angle with the ground, and the loading ramp itself is 14 feet long, then how far is the bottom of the ramp from the dock?

Solution: The loading ramp, the vertical side of the loading dock, and the ground make a 30-60-90 triangle. This is a classic triangle that comes from bisecting an equilateral triangle, so we know that the height of the dock is exactly half the length of the ramp. Thus, since the ramp is 14 feet long, the dock is 7 feet above the ground. Using the Pythagorean theorem, and calling the bottom of the triangle x we know that

\(\begin{align}x^2 + 7^2 = 14^2\end{align}\)
\(\begin{align}x^2 = 14^2 – 7^2 = (14 + 7)(14 – 7) = 21 · 7 = 3 · 7^2\end{align}\)
\(\begin{align}x^2 = 3 · 7^2 \end{align}\)

Therefore,

\(\begin{align}x = 7 \sqrt{3} \end{align}\)

This is how far the bottom of the ramp is from the dock.

Example 2: A stained glass window looks like the diagram shown. The center portion is a square and shows a large picture, and it’s surrounded by small squares, depicting smaller versions of the large picture. If the area of the square in the center is 6400 in2, what is the area each of the smaller surrounding squares?




Solution:
Since the area of the square in the center is 6400 in², each side of that square must by 80 inches. Also, there are 4 smaller squares along each side, so each of them must have sides that are 20 inches long. So, their area is 400 in² each.

 

Interest and Interest Rate Problems

Formulas for one year’s interest:

Simple interest:

\(\begin{align}EndBalance = (1 + IntRate) \times BeginningBalance \end{align}\)

Compound interest:

\(\begin{align}EndBalance = (1 + \frac{IntRate}{n})^kn \times BeginningBalance \end{align}\)

where n is the number of times interest is compounded during a year, and k is the number of years compounding takes place during the period under consideration.

With simple interest, we have an interest rate, a time period, and a principal amount, and the problem may be to calculate how much interest is earned on the principal amount, without calculating interest on the interest. With compound interest we assume that the interest is added to the principal and so the computation of additional interest must consider the interest that has already accumulated.

 

Example 1: Ingrid deposits $1000 at simple interest in a savings account at the bank. After 1 year, during which she made no withdrawals and added no more to the account, she has $1062.50. What was the interest rate paid during this year?

Solution: If the simple interest rate is x, then the amount in the account after 1 year will be (1 + x) · 1000, and we’re told that this is equal to $1062.50. So

(1 + x) · 1000 = 1000 + 1000x = 1062.50 1000x = 62.50 x = 62.50/1000 = .0625 = 6.25%

Example 2: Ingrid deposits $1000 in another account and gets compound interest at 6% annually, compounded semi-annually. How much is in the account after 1 year?

Solution: In this case Ingrid is getting some interest on her interest. Since the interest is compounded semi-annually, we must do two calculations to get the result after 1 year. This compounding happens every 6 months, so the interest paid at that time is for just half a year. That means the interest rate at compounding time is half of 6%, which is 3%. Notice that n = 2 and k = 1 in this example.

(1 + .06/2)² × 1000 = (1.03)² × 1000 = 1.03 × (1.03 × 1000) = 1.03 × 1030 = 1060.90

 

Mixture Problems

Formula:

\(\begin{align}NewPercent = \frac{Percent1 · Quantity1 + Percent2 · Quantity2}{Quantity1 + Quantity2}\end{align}\)

This formula is typically used to determine the percentage of some material in a solution, after two other solutions with varying percentages of the material are mixed together. However, it can be used more flexibly to solve more complex problems. Notice that in this formula we have 5 variables: NewPercent, Percent1, Quantity1, Percent2, Quantity2. If we’re given values for 4 of the variables, then we can find the 5th one.

Example 1:

Suppose a 4 pound sack of mixed nuts contains 25% peanuts, and a 3 pound sack contains 40% peanuts. If the two sacks are combined, what will the percent of peanuts be in the combined sack?

Solution: We can apply the formula directly.

New percentage = (.25 × 4 + .4 × 3)/(4 + 3) = (1 + 1.2)/7 = 2.2/7 = .31 = 31%

Example 2: A goldsmith has two alloys of gold. The first alloy is 50% pure, and the second alloy is 75% pure. How many ounces of the 50% alloy must be mixed with the 75% alloy to make 100 ounces of an alloy that’s 66% pure gold?

Solution: This problem is more challenging because the information we need is disguised. We need x ounces of the 50% alloy and 100 ounces altogether. Thus, quantity1 = x, quantity1 + quantity2 = 100, and quantity2 = 100 – x. From this we get an equation which we need to solve for x:

.66 = (.5x + .75(100 – x))/100
.66 × 100 = .5x + 75 – .75x
66 = 75 – .25x

.25x = 75 – 66 = 9
x = 9/.25 = 36
100 – x = 64

So we need 36 ounces of the 50% alloy and 64 ounces of the 75% alloy to get 100 ounces of 66% alloy.

 

Profit/Loss Problems

Formula:

\(\begin{align}Profit = Revenue – Expense\end{align}\)

Example 1: If Electrons Unlimited sold a shipment of 30 computers for $250 each, and if the computers originally cost $180 each, what was their total profit on the sale of these computers?

Solution: Profit = Revenue – Expense The simplest approach to this problem is to calculate the profit on the sale of each computer and multiply the result by 30. So

Profit = (250 – 180) × 30 = 70 × 30 = $2100

Example 2: Electrons Unlimited got another shipment of 20 computers for $200 each, of which they sold 15 for $300. They then reduced the price to $250 and sold the remainder. What was their total profit on the 20 computers, considering only the original cost?

Solution: Their original expense was

Expense = 20 × 200 = 4,000


Their revenue came in two periods – the $300 period and the $250 period. The total for these two times was

Revenue = 15 × 300 + 5 × 250 = 4,500 + 1,250 = 5,750

Thus,

Profit = 5,750 – 4,000 = 1,750

 

Distance/Rate/Time Problems

Formula:

\(\begin{align}Distance = Rate \times Time \end{align}\)

At the simplest level these problems deal with the relationship between time, distance, and speed, using the formula distance = rate × time. But this idea can be generalized to apply to any proportional relationship that’s linear.

Example 1: Keith took a trip of 300 miles. He averaged 50 miles per hour for the first 100 miles, 70 for the next 140 miles, and 60 for the last 60 miles. What was his average speed for the trip?

Solution: We will use the formula Distance = Rate × Time to determine the rate. We already know the distance is 300, so we have to determine the total time. The first 100 miles took 2 hours, because he averaged 50 miles per hour. The second 140 miles also took 2 hours, because he averaged 70. And the last 60 miles took 1 hour, because he averaged 60. Therefore, the entire trip took 5 hours. So we have

Distance = Rate × Time 300 = Rate × 5 300/5 = 60 = Rate

That is, the average speed was 60 miles per hour.

Example 2: Meredith sold 14 insurance policies during January, February, and March. If she continues at this rate, during which month will she sell her 50th policy for the year?

Solution: In the first 3 months of the year, Meredith’s rate of selling policies has been 14/3 per month. To apply the formula we need to think of the distance as 50, and we need to find the month during which she will sell her 50th. Plugging into the formula in this situation we get

50 = 14/3 × Time
150/14 = Time
10 10/14 = Time

In other words, it will take her 10 and 10/14 months to sell 50 policies. That is, she will sell her 50th policy in the 11th month, November.

 

Applications of Set Concepts

Formulas:

A and B are sets. The cardinality of a set is the number of elements in the set.

|A ∪ B| = |A| + |B| – |A ∩ B| Cardinality of A ∪ B
|A ∩ B| = |A| + |B| – |A ∪ B| Cardinality of A ∩ B
|A – B| = |A| – |A ∩ B| Cardinality of set difference A – B

These problems use the basic ideas of combining sets. Venn diagrams show how several sets overlap, and we may be asked to determine how many items are in every set (set intersection), how many are in one set but not in any of the others (set difference), or how many are in the sets altogether (set union).

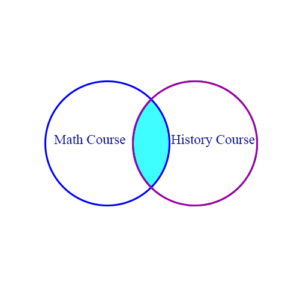
Example 1: 300 students are enrolled in a math course or a history course. 210 of them are taking the history course, and 135 are taking the math course. How many are taking both the math course and the history course?

Solution: The Venn diagram shows two sets of students as circles, with the circle on the left containing the students taking the math course and the circle on the right containing the students taking the history course.

The total number of students is 300, which means that the union of the two sets, written

MathCourse ∪ HistoryCourse

has 300 students in it. This is written

|MathCourse ∪ HistoryCourse| = 300

Now the question asks us how many students are taking both courses. This is the number of students in the shaded part of the diagram which identifies the overlap between the two sets. This is the intersection of the sets. The number of students in this intersection is written

|MathCourse ∩ HistoryCourse|

This is calculated by adding together the number of students who are individually taking each of the two courses, 135 and 210, and subtracting the total number of students, 300. Or, in other words

|MathCourse ∩ HistoryCourse| =
|MathCourse| + |HistoryCourse| – |MathCourse ∪ HistoryCourse| =
135 + 210 – 300 = 45

So the number of students taking both courses is 45.

Example 2: Same situation as example 1. How many students are taking the math course but not the history course?

Solution: In this case we want the cardinality of the set difference, MathCourse – HistoryCourse.

|MathCourse – HistoryCourse| = |MathCourse| – |MathCourse ∩ HistoryCourse|

|MathCourse – HistoryCourse| = 135 – 45 = 90

90 students are taking the math course but not the history course.

Sample Set Concepts Problems

 

Task/Job Problems

Formula:

\(\begin{align}\frac{1}{TotalTime} = \frac{1}{Time1} + \frac{1}{Time2} \end{align}\)

In these problems we look at tasks that are straightforward and whose completion rate is predictable. Usually, they are tasks involving repetitious labor which can be done either by humans or by machines. Examples might be painting a room, copying/printing documents, addressing envelopes, etc. The problems involve determining how fast a job can get done, for example, if multiple people are working, and we know how fast each one works. Or it might be the opposite, in the sense that if we know how fast two machines can get a job done, then we’re asked to determine how long it would take for one of the machines to do the entire job by itself. The formula given above should be viewed as a tool to be applied appropriately as the problem itself requires. We illustrate this in the examples. The basic idea of the formula is illustrated in the examples.

Example 1: Jon can paint a room by himself in 3 hours and Phil can do it alone in 6 hours. How many hours will it take them to do it together?

Solution: Applying the formula directly, we get this equation.

1/x = 1/3 + 1/6

Notice that we put in x in the denominator of the first fraction, because that’s the unknown quantity. But what does the equation mean? We know that Jon can do the job in 3 hours, so 1/3 represents the portion of the job he can do in one hour. That is, he can do 1/3 of the job in 1 hour. Phil then can do 1/6 of the job in 1 hour. And working together they can do 1/3 + 1/6 of the job in one hour. Let’s solve the equation for x and continue our explanation.

1/x = 1/3 + 1/6 = 2/6 + 1/6 = 3/6 = 1/2

That is, 1/x = 1/2, so x = 2. We conclude, therefore, that the formula is capturing the portion of the job that the two working together can accomplish in one hour. In this case, they get 1/2 of the job done in an hour, so working together they can get it done in 2 hours.

Now let’s change the numbers and see what happens. Suppose Jon can do the job in 3 hours and Phil in 4. Then we have

1/x = 1/3 + 1/4 = 4/12 + 3/12 = 7/12
1/x = 7/12
x = 12/7

So the job will be done in 12/7 or 1 5/7 hours when the two work together. Notice that we still just invert the two fractions, 1/x and 7/12, to get the desired result, 12/7.

Example 2: Jon can paint a room by himself in 3 hours, and Jon and Phil together can do the job in 1 7/8 hours. How long would it take Phil to paint the room by himself?

Solution: Again we use the formula, but this time we put the unknown value in a different place. We observe first of all that 1 7/8 is the same as 15/8, which inverted is 8/15.

8/15 = 1/3 + 1/x
8/15 – 1/3 = 1/x
8/15 – 5/15 = 3/15 = 1/5 = 1/x
5 = x

That is, Phil can paint the room by himself in 5 hours.

The point of this example is to show that we use the formula as a tool to find the solution to the problem. In this case, we needed to know where to put the unknown value – the x – in order to properly solve the problem.

More generally, if we’re working with different units of time, like days or weeks, then the formula is capturing the portion of the job that will be accomplished in one unit of whatever units of time we’re working with.

Unit Conversion Problems

Unit conversion problems involve going from one unit to another in the same measuring system, like the metric or the English systems.

Example 1: During a game a 278 pound professional football player runs 40 yards in 5 seconds. To the nearest mile, what is his average speed in miles per hour? (There are 1760 yards in a mile.)

Solution: We first determine what portion of a mile 40 yards is. To do this, we divide 1760 by 40:

1760/40 = 44

Now multiply 5 seconds by 44 to obtain the length of time it would take him to run a full mile at this rate:

5 × 44 = 220 seconds

There are 3600 seconds in an hour, so we now divide 3600 by 220:

3600/220 = 16.36

So, if he kept running at this rate for a full hour, he would travel 16.36 miles. Thus, his average speed to the nearest mile is 16 miles per hour.

Example 2: Helmut is riding his bike on a 126 kilometer trip. If he averages 7 meters/second, how many hours will the trip take? (There are 1000 meters in a kilometer.)

Solution: 126 kilometers is 126,000 meters. So the number of seconds the trip will take is

126,000/7 = 18,000

There are 3,600 seconds in an hour, so the number of hours required is

18,000/3,600 = 5

Or, solving a different way, we determine how far he can go in an hour.

7 × 3,600 = 25,200

And

126,000/25,200 = 5

More Sample Word Problems